Basic knowledge of high frequency circuits

Why should we learn about high-frequency circuits?
Electronic circuits can be divided into analog circuits and digital circuits, and analog circuits can be further divided into low-frequency circuits and high-frequency circuits.
Most electronic technicians first try to design or produce digital circuits or low-frequency circuits, and rarely start with high-frequency circuits. The main reason is that high-frequency circuits are more difficult to understand, and the circuits produced often fail to operate as expected.
However, if the basic knowledge of high-frequency circuits is ignored, the designed digital circuits or low-frequency circuits may not be the most appropriate, and may even cause unstable operation.
On the contrary, if you are familiar with high-frequency circuits, you can also improve the design level of digital circuits or low-frequency circuits. In recent years, whether it is digital circuits or DC-based test instrument circuits, the processing system requires high speed, which makes the basic knowledge of high-frequency circuits very important.

Difference between low frequency circuit and high frequency circuit
In order to understand the characteristics of high frequency circuit, here, we will compare low frequency circuit and high frequency circuit. The following figure 1 shows the comparison between low frequency circuit and high frequency circuit. Figure (a) is a low frequency circuit, and Figure (b) is a high frequency circuit. First, the flow of signals is explained. Since the wavelength of the signal in the low frequency circuit is longer, the time factor can generally be ignored. Therefore, the output end of the oscillator and the input end of the amplifier can be regarded as the same signal. In other words, the signal flow in the low frequency circuit is as shown in the direction of the arrow, forming a closed loop, which is also called the method of considering the concentrated constant. In the high frequency circuit, due to the shorter wavelength, the time factor cannot be ignored. At the same time, the signal at the output end of the oscillator, the signal at the input end of the amplifier on the cable in the middle is not the same signal, that is, the signal is transmitted like an electric wave, and this method of considering circuit problems is called a distributed constant.
Generally, in the low frequency circuit in the concentrated constant circuit, there are fewer restrictions on the cable, and general isolation lines can be used, and the noise-induced frequency characteristics are emphasized. In the high-frequency circuit of the distributed constant circuit, in order to prevent the signal from being distorted in the transmission path, a coaxial cable is used and the characteristic impedance is emphasized.
The load connected to the output of the amplifier is as follows:

Lumped Constant Circuits and Distributed Constant Circuits

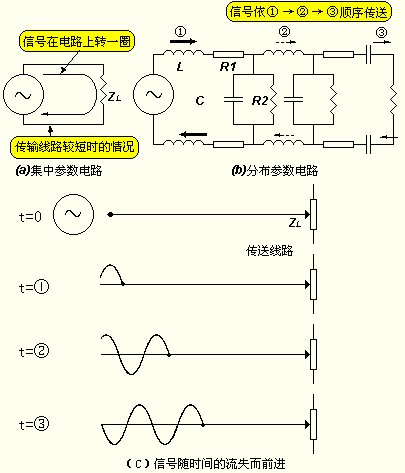
The figure on the right shows the analysis method of the concentrated constant circuit and the distributed constant circuit using the transmission path as an example.

In fact, no matter what low-frequency or high-frequency circuit, there are resistors R, capacitors C, and coils L. However, as shown in Figure (a), when the transmission path is very short or in the field of low-frequency signals, the existence of R, L, and C can be ignored and treated as concentrated constants. In this way, the circuit analysis can be simplified. In
the case of Figure (b), when the transmission path is long or in the field of high-frequency signals, the existence of R, L, and C cannot be ignored. As time passes, the signal will advance in the transmission path (route) in the situation of ①→②→③.