Detailed explanation of the calculation of MOSFET power consumption in high-power power supplies

Power MOSFETs are the main building blocks of high-power switching power supplies in portable devices. In addition, these MOSFETs are the most difficult components to determine in notebook computers where heat dissipation is extremely low.

This article provides steps to calculate the power dissipation in MOSFETs and determine their operating temperature. It also explains these concepts in detail with an example of distributed calculations for a single 30A phase in a multiphase, synchronously rectified, step-down CPU core power supply.

Perhaps the most daunting challenge facing today's portable power designers is providing power to today's high-performance CPUs. CPU supply current has doubled every two years recently. In fact, today's portable core power supplies can demand 60A or more at voltages between 0.9V and 1.75V. However, despite the steady increase in current demands, the headroom available for the power supply has not increased—a reality that has reached the limits of thermal design and exceeded.

Such high current supplies are usually split into two or more phases, each providing 15A to 30A. This approach makes component selection easier. For example, a 60A supply becomes two 30A supplies. However, this approach does not add additional board space and does little to help with thermal design challenges.

MOSFETs are the most difficult components to determine when designing high-current power supplies. This is especially true in laptops, where heat sinks, fans, heat pipes, and other cooling methods are usually reserved for the CPU. As a result, power supply designs are often challenged by tight spaces, stagnant airflow, and heat from other nearby components. And, aside from a small amount of printed circuit board copper underneath the power supply, there is nothing else to help dissipate the power.

When selecting a MOSFET, the first thing to do is to select a device with sufficient current handling capability and sufficient heat dissipation paths. Finally, the necessary heat dissipation must be quantified and sufficient heat dissipation paths must be ensured. This article will explain step by step how to calculate the power dissipation of these MOSFETs and determine their operating temperature. Then, by analyzing

The following is a design example of a 30A single-phase multiphase, synchronous rectification, step-down CPU core power supply to further illustrate these concepts.

To determine whether a MOSFET is suitable for a particular application, you must calculate its power dissipation, which consists mainly of resistive and switching losses:

PD _{DEVICE TOTAL} = PD _RESISTIVE + PD _SWITCHING

Since the power dissipation of a MOSFET depends largely on its on-resistance (R _DS(ON) ), calculating R _DS(ON) seems like a good starting point. But the MOSFET's R _DS(ON) is related to its junction temperature (T J ). That said, T _J depends on the MOSFET's power dissipation and the MOSFET's thermal resistance (Θ _JA ). It seems difficult to find a starting point. Since the calculation of power dissipation involves several interdependent factors, we can use an iterative process to get the results we need (Figure 1).

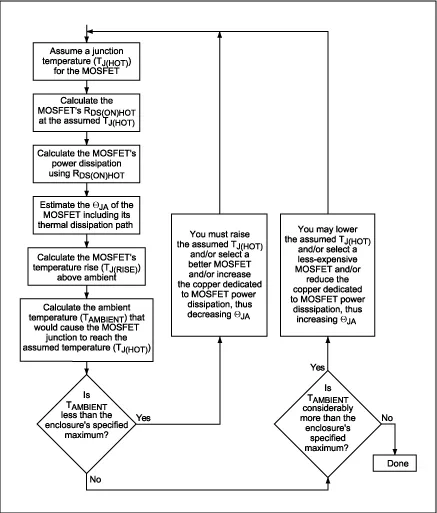
Figure 1. This flowchart shows the iterative process of selecting each MOSFET (synchronous rectifier and switching MOSFET). During this process, the junction temperature of each MOSFET is assumed, and the power dissipation and allowable ambient temperature of both MOSFETs are calculated. The process ends when the allowable ambient temperature reaches or slightly exceeds the maximum temperature we expect in the chassis (where the power supply and the circuits it drives are installed).

The iterative process begins by assuming a junction temperature for each MOSFET, then calculating the power dissipation and allowable ambient temperature for each MOSFET individually. The process ends when the allowable ambient air temperature is at or slightly above the expected maximum temperature of the chassis where the power supply and the circuit it drives are located.

Some people try to make this calculated ambient temperature as high as possible, but this is usually not a good idea. Doing so would require using more expensive MOSFETs, putting more copper under the MOSFETs, or requiring a bigger, faster fan to create airflow—all of which are undesirable.

In a sense, assuming an MOSFET junction temperature and then calculating the ambient temperature is a backwards approach. After all, the ambient temperature determines the MOSFET junction temperature—not the other way around. However, it is easier to start with an assumed junction temperature than with the ambient temperature.

For the switching MOSFET and synchronous rectifier, we can choose a maximum allowable die junction temperature (T _J(HOT) ) as a starting point for the iterative process. Most MOSFET data sheets only specify the maximum R _DS(ON) at +25°C , but some recent MOSFET documents also give a maximum value at +125°C. The R _{DS(ON) of a MOSFET} increases with temperature, with a typical temperature coefficient of 0.35%/°C to 0.5%/°C (Figure 2).

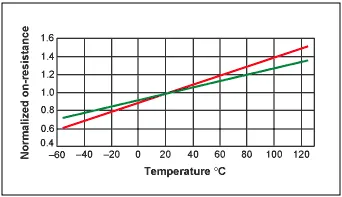
Figure 2. The temperature coefficient of on-resistance of a typical power MOSFET ranges from 0.35% per degree (green line) to 0.5% per degree (red line).

If in doubt, you can approximate the maximum R _{DS(ON) at a chosen T J(HOT} ) by using a worse temperature coefficient and the MOSFET's +25°C specification (or +125°C specification, if available) :

R _DS(ON)HOT = R _DS(ON)SPEC [1 + 0.005 × (T _J(HOT) - T _SPEC )]

Where R _DS(ON)SPEC is the on-resistance of the MOSFET used in the calculation and T _SPEC is the temperature at which R _DS(ON)SPEC is specified . Using the calculated R _DS(ON)HOT , the power dissipation of the synchronous rectifier and the switching MOSFET can be determined as follows.

In the following sections, we will discuss how to calculate the power dissipation of each MOSFET at a given die temperature, as well as the subsequent steps in the iterative process (the entire process is detailed in Figure 1).

In all but the lightest loads, the drain-source voltage of the synchronous rectifier MOSFET is clamped by the freewheeling diode during both the turn-on and turn-off processes. Therefore, the synchronous rectifier has almost no switching losses, and its power dissipation is easy to calculate. Only the resistive losses need to be considered.

The worst-case loss occurs when the synchronous rectifier operates at the maximum duty cycle, that is, when the input voltage reaches the maximum. Using the synchronous rectifier's R _DS(ON)HOT and the operating duty cycle, and using Ohm's law, we can approximate its power consumption:

PD _{SYNCHRONOUS RECTIFIER} = [I _LOAD ² × R _DS(ON)HOT ] × [1 - (V _OUT /V _INMAX )]

The calculation of the resistive losses of the switching MOSFET is very similar to that of the synchronous rectifier, and also uses its duty cycle (which is different from the former) and R _DS(ON)HOT :

PD _RESISTIVE = [I _LOAD ² × R _DS(ON)HOT ] × (V _OUT /V _IN )

The switching loss of a switching MOSFET is difficult to calculate because it depends on many factors that are difficult to quantify and usually not specified, which affect both the turn-on and turn-off processes. We can first evaluate a MOSFET using the following rough approximation formula and then verify its performance through experiments:

PD _SWITCHING = (C _RSS × V _IN ² × f _SW × I _LOAD )/I _GATE

where C _RSS is the reverse transfer capacitance of the MOSFET (a parameter in the data sheet), f _SW is the switching frequency, and I _GATE is the current that the MOSFET gate driver sinks/sources when the MOSFET is at critical conduction (V _GS is in the flat region of the gate charging curve).

Once the choice has been narrowed down to a particular generation of MOSFETs based on cost (the costs of different generations of MOSFETs vary greatly), we can then find a device within that generation that will minimize power dissipation. This device should have a balance of resistive and switching losses. Using a smaller (faster) MOSFET will increase resistive losses more than it reduces switching losses, while a larger (lower R _DS(ON) ) device will increase switching losses more than it reduces resistive losses.

If V _IN varies, the power dissipation of the switching MOSFET needs to be calculated at V _IN(MAX) and V _IN(MIN) . The worst case for the MOSFET power dissipation may occur at the minimum or maximum input voltage. This power dissipation is the sum of two factors: the highest resistive dissipation at V _IN(MIN) (higher duty cycle), and the highest switching loss at V _{IN(MAX) (due to the V IN} ² term). A good choice should have approximately the same dissipation at the two extremes of V _{IN , and maintain balanced resistive and switching losses over the entire V IN} range.

If the losses are significantly higher at V _IN(MIN) , then resistive losses dominate. In this case, consider using a larger switching MOSFET (or connecting more than one transistor in parallel) to reduce R _DS(ON) . However, if the losses are significantly higher at V _IN(MAX) , then consider reducing the size of the switching MOSFET (or removing one MOSFET if multiple transistors are connected in parallel) to make it switch faster.

If the resistive and switching losses are balanced but the total power dissipation is still too high, there are several ways to solve it:

It is not possible to fine-tune the size of the MOSFET out of a given condition because the range of device choices is limited. The bottom line is that the worst-case power dissipation of the MOSFET must be able to be dissipated.

The next step is to calculate the ambient temperature around each MOSFET, at which the MOSFET junction temperature will reach our assumed value

(The appropriate MOSFETs to use as the synchronous rectifier and the switching MOSFET are determined by the iterative process shown earlier in Figure 1.) To do this, the junction-to-ambient thermal resistance (Θ _JA ) of each MOSFET must first be determined.

_{Estimating thermal resistance can be difficult. It is relatively easy to calculate the θJA} of a single device on a simple PCB , but it is difficult to predict the thermal performance of an actual power supply in a system where there are many heat sources competing for limited heat dissipation paths. If multiple MOSFETs are used in parallel, the overall thermal resistance is calculated in the same way as calculating the equivalent resistance of two or more parallel resistors.

We can start with the MOSFET’s Θ _JA specification. For a single-die, 8-pin packaged MOSFET, Θ _JA is typically close to 62°C/W. Other package types, some with heat sinks or exposed thermal pads, typically have thermal resistances in the 40°C/W to 50°C/W range (Table 1).

Table 1. Typical thermal resistance of MOSFET packages

The temperature rise of the MOSFET die relative to the environment can be calculated using the following formula:

T _J(RISE) = PD _{DEVICE TOTAL} × Θ _JA

Next, calculate the ambient temperature that causes the die to reach a predetermined T _J(HOT) :

T _AMBIENT = T _J(HOT) - T _J(RISE)

If the calculated T _AMBIENT is lower than the maximum rated ambient temperature of the chassis (meaning that the maximum rated ambient temperature of the chassis will cause the predetermined T _J(HOT) of the MOSFET to be exceeded), one or more of the following measures must be taken:

Recalculate T _AMBIENT (using a quick calculation table can simplify the calculation process, and an acceptable design can be selected after several iterations.) On the other hand, if the calculated T _AMBIENT is much higher than the maximum rated ambient temperature of the enclosure, any or all of the following optional steps can be taken:

These last few steps are optional, because the MOSFET will not be damaged by overheating in this case. However, by doing these steps, we can reduce the board area and cost as long as T _AMBIENT is higher than the maximum temperature of the chassis by a certain margin.

The largest source of error in the above calculations comes from Θ _JA . You should read all the comments about the Θ _JA specification in the data sheet carefully . The general specification assumes that the device is mounted on 1 in² of 2 oz copper. The copper dissipates most of the power, and the Θ _JA varies greatly with the amount of copper. For example, a D-Pak package with 1 in² of copper will have a Θ _JA of 50°C/W. However, if the copper is placed only on the underside of the pins, the Θ _JA will be twice as high (Table 1).

If multiple MOSFETs are used in parallel, ΘJA _is mainly determined by the copper area they are mounted on. The equivalent ΘJA of two devices _can be half that of a single device, but the copper area must be doubled at the same time. In other words, adding a MOSFET in parallel without adding copper can halve RDS _(ON) without changing ΘJA _much .

Finally, the ΘJA _{specification} usually assumes that no other devices transfer heat to the copper film heat sink. However, at high currents, every component in the power path, even the PCB traces, will generate heat. To avoid overheating the MOSFET, it is necessary to carefully estimate the ΘJA in the actual situation _and take the following measures:

The CPU core power supply shown in Figure 3 provides a 1.5V/60A output. Two identical 30A power stages operating at 300kHz provide a total output current of 60A. The MAX1544 IC drives the two stages, operating 180° out of phase. The input range of this supply is 7V to 24V, and the maximum rated ambient temperature of the chassis is +60°C.

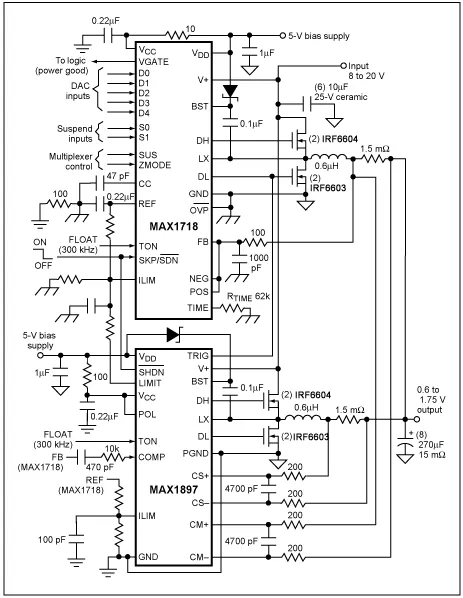
Figure 3. The MOSFETs in this step-down switching regulator were selected using the iterative process described in this article. Board-level designers typically use this type of switching regulator to drive today’s high-performance CPUs.

The synchronous rectifier consists of two IRF6603 MOSFETs in parallel, with a combined maximum R _DS(ON) of 2.75mΩ at room temperature and approximately 4.13mΩ at +125°C (predetermined T _{J(HOT) ). At a maximum duty cycle of 94%, 30A load current, and a maximum R DS(ON)} of 4.13mΩ , these parallel MOSFETs will dissipate approximately 3.5W. Providing 2in² of copper to dissipate this power, the overall Θ _JA is approximately 18°C/W, a value taken from the MOSFET data sheet. The combined MOSFET temperature rise will be close to +63°C, so the design should be able to operate up to an ambient temperature of +60°C.

The switching MOSFET consists of two IRF6604 MOSFETs in parallel. The maximum R _DS(ON) of the combined device is 6.5mΩ at room temperature and approximately 9.75mΩ at +125°C (predetermined T _J(HOT) ). The combined C _RSS is 380pF. The MAX1544's 1Ω high-side gate driver can provide nearly 1.6A of drive. At V _IN = 7V, the resistive losses are 1.63W and the switching losses are approximately 0.105W. At V _IN = 24V, the resistive losses are 0.475W and the switching losses are approximately 1.23W. The total losses are approximately equal at each input operating point, with the worst-case (lowest V _IN ) total losses being 1.74W.

_{A ΘJA} of 28°C/W will produce a temperature rise of +46°C, allowing operation up to an ambient temperature of +80°C. If the ambient temperature is higher than the maximum specified temperature of the package, the designer should consider reducing the copper area used for the MOSFET, although this step is not required. The copper area in this example is only considered for the MOSFET alone. If there are other devices that are cooling this area, more copper area may be required. If there is not enough space

By increasing the copper coverage, you can reduce the overall power consumption, transfer the heat to a lower dissipation area, or use active methods to move the heat away.

Thermal management is one of the more challenging areas of high-power portable design. This difficulty makes it necessary to use the iterative process described above. Although this process can lead the board-level designer closer to the final design, it is necessary to conduct experiments to ultimately determine whether the design process is accurate enough. Calculating the thermal performance of the MOSFETs, providing them with adequate dissipation paths, and then verifying these calculations in the lab will help to obtain a robust thermal design.

Source: Analog Devices

· END ·

You are welcome to set us as “ Star ” so that you can receive push messages as soon as possible.

Scan the QR code to follow: Automotive Development Circle, reply " Auto "

Get free information packages on Autosar architecture, standards and systems, application development, etc.!

Scan the QR code to add the assistant and reply "join the group"

Exchange experiences with electronic engineers face to face