How to understand circuit diagrams (VI): Detailed explanation of digital logic circuits

The rising star in digital electronic circuits is the digital logic circuit. It is called a digital circuit because although the pulses transmitted in the circuit are also pulses, these pulses are used to represent binary digits, for example, a high level represents "1" and a low level represents "0". After digital processing, information such as sound, image, and text becomes a series of electrical pulses, which are called digital signals. Circuits that can process digital signals are called digital circuits.

　　This circuit is also called a logic circuit because the "1" and "0" in the circuit also have logical meanings. For example, logic "1" and logic "0" can represent the connection and disconnection of the circuit, the yes and no of an event, the true and false of logical reasoning, etc. There is a logical relationship between the output and input of the circuit. In addition to binary arithmetic operations, this circuit can also perform logical operations and have logical reasoning capabilities, so it is called a logic circuit.

　　Since digital logic circuits have the advantages of easy integration, high transmission quality, and the ability of calculation and logical reasoning, they are widely used in the fields of computers, automatic control, communication, measurement, etc. In general household appliances, such as timers, alarms, controllers, electronic clocks, electronic toys, etc., digital logic circuits are used.

　　The first characteristic of digital logic circuits is that they use unique graphic symbols to highlight the word "logic". There are two basic unit circuits in digital logic circuits: gate circuits and triggers. They are both composed of components such as transistors and resistors, but in logic circuits we only use a few simplified graphic symbols to represent them, without drawing their specific circuits, regardless of how high the voltage is, whether it is a TTL circuit or a CMOS circuit, etc. The diagram drawn by combining these graphic symbols according to the requirements of logical functions is a logic circuit diagram, which is completely different from the general amplification oscillation or pulse circuit diagram.

　　The relevant information in the digital circuit is contained in the digital combination of 0 and 1, so as long as the circuit can clearly distinguish 0 and 1, and the combination relationship of 0 and 1 is not destroyed, we don’t care much about the quality of the pulse waveform. Therefore, the second characteristic of digital logic circuits is that we are mainly concerned about what kind of logical functions it can complete, and rarely consider its electrical parameter performance and other issues. For this reason, some special expression methods such as truth tables, characteristic equations, etc. are used in digital logic circuits, and some special analysis tools such as logic algebra, Karnaugh maps, etc. are also used, which are also different from amplification and oscillation circuits.

　　Gates and flip-flops

　　(1) Gate circuit

　　Gate circuits can be considered the simplest components in digital logic circuits. Currently, there are a large number of integrated products available.

　　There are three basic gate circuits: NOT gate, AND gate and OR gate. NOT gate is an inverter, which turns the input 0 signal into 1 and 1 into 0. This logic function is called "NOT". If the input is A, the output is written as P=A. AND gate has more than 2 inputs, and its function is that when the inputs are all 1, the output is 1. This function is also called logical multiplication. If the inputs are A and B, the output is written as P=A·B. OR gate also has more than 2 inputs, and its function is that when one of the inputs is 1, the output is 1. This function is also called logical addition, and the output is written as P=A + B.

　　Combining these three basic gate circuits can produce various composite gate circuits, such as AND gate plus NOT gate to form NAND gate, OR gate plus NOT gate to form NOR gate. Figure 1 shows their graphic symbols and truth tables. In addition, there are AND-NOR gate, XOR gate, etc.

　　

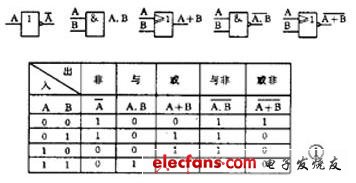
　　Digital integrated circuits include TTL, HTL, CMOS, etc., and the power supply voltage and polarity used are also different, but as long as they have the same logical function, they use the same logic symbol. And generally, high level is 1 and low level is 0.
(2) Trigger

　　A trigger is actually a bistable circuit in a pulse circuit. Its circuit and function are more complex than gate circuits. It can also be regarded as a component in a digital logic circuit. Currently, integrated products are available. Commonly used triggers include D triggers and J-K triggers.

　　The D flip-flop has an input terminal D and a clock signal input terminal CP. An arrow is added to the CP terminal to distinguish it. It has two output terminals, one is Q and the other is Q. The output terminal with a small circle is the Q terminal. In addition, it has two preset terminals RD and SD. During normal operation, both RD and SD terminals must be added with a high level 1. If RD = 0 (SD is still 1), the flip-flop is set to Q = 0; if SD = 0 (RD = 1), it is set to Q = 1. Therefore, the RD terminal is called the set 0 terminal, and the SD terminal is called the set 1 terminal. The logic symbol of the D flip-flop is shown in Figure 2. In the figure, the Q, D, and SD terminals are drawn on the same side; Q and RD are drawn on the other side. RD and SD are both circled, indicating that a low level must be added to be effective.

　　

　　The D flip-flop is controlled by both CP and D terminals. When CP is high level 1, its output is the same as the state of D. For example, if D=0, after CP comes, Q=0; if D=1, after CP comes, Q=1. The CP pulse controls the opening of the gate. If CP=0, no matter what state D is in, the flip-flop maintains its original state. Such a logical function is drawn into a table called a function table or a characteristic table, as shown in Figure 2. In the table, Qn+1 indicates the state after the trigger signal is added, and Qn is the original state. "X" indicates any state of 0 or 1.

　　Some D flip-flops have several D input terminals: D1, D2..., which have a logical AND relationship with each other. That is, only when D1, D2... are all 1, the output terminal Q is 1.

　　Another type of trigger with better performance is called J-K trigger. It has two input terminals: J and K, one CP terminal, two preset terminals: RD and SD, and two output terminals: Q and Q. Its logic symbol is shown in Figure 3. The J-K trigger is triggered to flip on the falling edge of the CP pulse, so a small circle is drawn on the CP terminal to distinguish it. In the figure, J, SD, and Q are drawn on the same side, and K, RD, and Q are drawn on the other side.

　　

　　The logic function of the J-K flip-flop is shown in Figure 3. When there is a CP pulse (i.e. CP=1): J and K are both 0, and the state of the flip-flop remains unchanged; Qn+1=Qn, J=0, K=1, the flip-flop is set to 0: Qn+1=0; J=1, K=0, Qn+1=1; J=1, K=1, the flip-flop flips: Qn+1=Qn. If no clock pulse is added, i.e. CP=0, no matter what the state of the J and K terminals is, the flip-flop maintains its original state: Qn+1=Qn. Some J-K flip-flops have several J terminals and K terminals at the same time, and the relationship between J1, J2... and K1, K2... is logical AND. Some J-K flip-flops are triggered to flip on the rising edge of CP, and in this case, the CP terminal of its logic symbol diagram does not have a small circle. Sometimes, in order to make the diagram more concise, the RD and SD terminals are often omitted.

　　A circuit that can convert numbers and letters into binary digits is called an encoder. Conversely, a circuit that can convert binary digits back into numbers and letters is called a decoder.

　　(1) Encoder

　　Figure 4 (a) is an encoder that can convert decimal numbers into binary code. A decimal number needs 4 bits to be represented as binary code. The commonly used code is to make each bit of binary code from low to high equivalent to

　　The decimal numbers 1, 2, 4, 8 are called 8-4-2-1 code or BCD code for short. So this encoder is called "10-line-4-line encoder" or "DEC/BCD encoder".

　　As can be seen from the figure, it is composed of NAND gates. There are 10 input terminals, which are controlled by buttons. Usually, the button is left floating, which is equivalent to connecting a high level 1. It has 4 output terminals ABCD, which output 8421 code. If the "1" key is pressed, the line corresponding to the "1" key is grounded, which is equivalent to inputting a low level 0, so the output of gate D is 1, and the entire output becomes 0001.

　　

　　If the "7" key is pressed, the outputs of gates B, C, and D are 1, and the entire output is 0111. If these circuits are all built into an integrated chip, an integrated 10-line 4-line encoder is obtained. Its logic symbol is shown in Figure 4 (b). There are 10 input terminals on the left, with small circles indicating that low level is required. There are 4 output terminals on the right, arranged from top to bottom from low to high. It can be directly selected when used.
(2) Decoder

　　To convert binary code into decimal number, a decoder is needed. It is also composed of gate circuits, and now there are integrated products for selection. Figure 5 is a 4-line to 10-line decoder. Its left side is the input end of 4 binary codes, and the right side has 10 output ends, which are arranged from top to bottom as 0, 1, ...9 to represent 10 decimal numbers. The output end with a small circle indicates that the low level is valid. Usually, all 10 output ends are high level 1. For example, if the input is 1001 code, the output "9" end is low level 0, and the other 9 lines are still high level 1, which means that the "9" line is decoded.

　　If each segment of the diode is connected to a low level 0, all seven segments will light up and display the number "8"; if segments b and c are connected to a low level 0 and the rest are connected to 1, the display will be "1". It can be seen that in order to display a decimal number with a seven-segment display tube, it is necessary to go through a decoding process. If a "4-line-7-line decoder" is used in conjunction with a display tube, it is very simple. The input binary code can directly display the decimal number, as shown in Figure 6. There are 4 binary code input terminals on the left side of the decoder, and 7 outputs on the right side that can be directly connected to the digital tube. There is another light-off control terminal IB on the upper left side. When working normally, a high level 1 should be added. If this digit is not needed to be displayed, a low level 0 is added to IB to turn off this digit.

　　

　　If you want to display decimal numbers, you need to use a digital tube. Take the common anode light emitting diode (LED) seven-segment digital display tube as an example, see Figure 6. It has seven segments of light

　　

　　Registers and Shift Registers

　　(1) Register

　　The component that can store binary digits is called a digital register, or register for short. Figure 7 shows a register composed of 4 D flip-flops, which can store 4-bit binary numbers. The 4 CP terminals are connected together as the control terminal, and it only receives and stores digits when CP=1. The 4 RD terminals are connected together to become the clear terminal of the entire register. If you want to store the binary code 1001, just add them to the D terminal of the flip-flop respectively. When CP comes, the 4 flip-flops are set to 1, 0, 0, 1 from high to low, and remain until the next input data. To take out this string of digits, you can take it out from the Q terminal of the flip-flop.

　　

　　(2) Shift register

　　A register with shift function is called a shift register. It can shift left, right, or bidirectionally.

　　Figure 8 is a register that can shift digital data bit by bit to the left. It is different from general registers in that digital data is serially input bit by bit and added to the lowest bit D terminal, and then the low bit Q terminal is connected to the high bit D terminal. At this time, CP is called a shift pulse.

　　

　　First, send a low level from the RD end to clear the register to 0000. Assuming that the digital number to be input is 1001, the input order is high first and low bit by bit. After the first CP, 1 is entered into the first trigger, and the register becomes 0001; after the second CP, the 1 of Qo is moved into Q1, and the new 0 is entered into D1, becoming 0010; after the third CP, it becomes 0100; after the fourth CP, it becomes 1001.

　　It can be seen that after 4 CPs, the register stores the 4-bit binary code 1001. Currently, there are many types of integrated registers available for selection.
Counters and frequency dividers

　　(1) Counter

　　The component that can count pulses is called a counter. There are many kinds of counters, including those that count cumulatively, called adder counters, and those that count decrementally, called subtractor counters; according to the flip-flop, there are synchronous counters and asynchronous counters; according to the number system, there are binary counters, decimal counters, and other radix counters, etc.

　　Let's take the simplest adder counter as an example, see Figure 9. It is a hexadecimal counter with a maximum count value of 1111, which is equivalent to the decimal number 15. The pulse to be counted is added to the CP terminal of the lowest bit flip-flop, all J and K terminals are connected to the high level 1, and the Q terminal of each flip-flop is connected to the CP terminal of the adjacent higher bit flip-flop. The characteristic table of the J-K flip-flop tells us: when J=1 and K=1, a CP comes, and the flip-flop flips once. After all are cleared, ① at the first CP trailing edge, the flip-flop C0 flips to Q0=1, and the other three flip-flops remain in the 0 state, and the state of the entire counter is 0001. ② at the second CP trailing edge, the flip-flop C0 flips to "Q0=0 again, C1 flips to Q1=1, and the counter becomes 0010. ... At the 15th CP trailing edge, the counter becomes 1111. It can be seen that this counter can indeed count CP pulses.

　　

　　(2) Frequency divider

　　The first trigger of the counter sends out a carry pulse every 2 CPs, so each trigger is a 2-divide frequency divider, and the hexadecimal counter is a 16-divide frequency divider.

　　In order to improve the accuracy of electronic clocks, the commonly used method is to use crystal

　　The 32768 Hz standard signal pulse is generated, and the 1 Hz second signal is obtained after 15 levels of 2-frequency division. Because the accuracy and stability of the crystal oscillator are very high, the obtained second pulse signal is also accurate and reliable. Putting them on an integrated chip is an electronic watch special integrated circuit product, as shown in Figure 10.

　　
Key points and examples of reading digital logic circuit diagrams

　　The steps for reading the diagram of digital logic circuits are the same as those for other circuits, except that the logic analysis method must be used everywhere when analyzing the circuit. When reading the diagram, you should: ① First have a general understanding of the purpose and performance of the circuit.

　　② Find the input, output and key components, distinguish various signals and figure out the direction of signal flow.

　　③ Analyze the logical relationship between output and input step by step and understand the logical functions of each part.

　　④ Finally, take a comprehensive look at the overall situation and draw the analysis results.

　　Example 1: Three-way buzzer

　　Figure 11 is a three-way buzzer circuit for quiz competitions. The referee presses switch SA4, and all triggers are reset to zero, entering the ready state. At this time, Q1 ~ Q3 are all 1, and the buzzer light is off; the outputs of gates 1 and 2 are 0, the audio oscillator composed of gates 3 and 4 does not oscillate, and the speaker is silent.

　　

　　At the beginning of the competition, assume that station 1 presses SA1 first, and trigger C1 flips to Q1=1, Q1=0. Then: ① Gate 2 outputs 1, the oscillator oscillates, and the speaker sounds; ② HL1 lights up; ③ Gate 1 outputs 1, and then stations 2 and 3 press the switch and it does not work. After the referee announces the result of the competition, press SA4 again, and the circuit enters the ready state again.

　　Example 2: Colored light chasing circuit

　　Figure 12 is a colored light circuit controlled by a 4-bit shift register. At the beginning, SA is pressed, and the triggers C1 to C4 are set to 1000, and the colored light HL1 is lit. After the CP pulse arrives, the register shifts 1 bit, the triggers C1 to C4 become 0100, and the colored light HL2 is lit. The second CP pulse lights up HL3, the third lights up HL4, and the fourth CP sets the triggers C1 to C4 to 1000, and lights up HL1 again. This cycle repeats, and the colored lights keep flashing. As long as the number of triggers is increased, the number of lights can be increased, and the speed can be changed by changing the frequency of CP.