pid controller principle

In engineering practice, the most widely used regulator control law is proportional integral differential control, referred to as PID control, also known as PID regulation. It has been nearly 60 years since the PID controller came out. It has become an important and reliable technical tool for industrial control due to its simple structure, good stability, reliable operation and convenient adjustment. When the structure and parameters of the controlled object cannot be fully grasped, or an accurate mathematical model cannot be obtained, other design techniques of control theory are difficult to use. The structure and parameters of the system controller must be determined by experience and on-site debugging. It is most convenient to apply PID control technology. That is, when we do not fully understand a system and the controlled object, or cannot obtain the parameters of the system through effective measurement methods, PID control technology is most suitable.

Proportional-integral-derivative control consists of three parts: proportional, integral, and differential. In practice, there are also PI and PD controllers. The PID controller uses proportional integral differential to calculate the control quantity based on the system error. Figure 1.2a shows a PID control structure diagram. The relationship between the controller output and the controller input (error) is available in the time domain. Formula (1.2a) is expressed as follows:

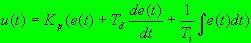(1.2a)

The formula represents the error and the input of the controller, is the output of the controller, is the proportional coefficient, is the integral time constant, and is the differential time constant. (1.2a) can also be expressed as:

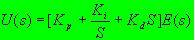(1.2b)

In the formula , and are the Laplace transforms of and respectively , . , , are the proportional, integral and differential coefficients of the controller respectively.

Proportional (P) control

Proportional control is the simplest control method. The controller's output is proportional to the input error signal. When there is only proportional control, there is a steady-state error in the system output.

Integral (I) control

In integral control, the output of the controller is proportional to the integral of the input error signal.

For an automatic control system, if there is a steady-state error after entering the steady state, the control system is said to have a steady-state error or simply a system with a difference (System with Steady-state Error). In order to eliminate the steady-state error, an "integral term" must be introduced in the controller. The integral term integrates the error with respect to time. As time increases, the integral term will increase. In this way, even if the error is small, the integral term will increase as time increases, which promotes the controller's output to increase and further reduce the steady-state error until it is equal to zero.

Therefore, the proportional + integral (PI) controller can make the system free of steady-state errors after entering the steady state.

Derivative (D) control

In differential control, the output of the controller is proportional to the differential of the input error signal (i.e., the rate of change of the error).

Automatic control systems may oscillate or even become unstable during the adjustment process to overcome errors. The reason is that due to the existence of components (links) with large inertia and/or components with lag (delay), trying to overcome the effect of errors, their changes always lag behind the changes in errors. The solution is to make the change in the effect of overcoming the error somewhat "ahead", that is, when the error is close to zero, the effect of overcoming the error should be zero. That is to say, it is often not enough to only introduce the "proportional" term in the controller. The function of the proportional term is only to amplify the amplitude of the error. What needs to be added now is the "differential term", which can predict the trend of error changes. In this way, a controller with proportional + differential can make the control effect to overcome the error equal to zero or even a negative value in advance, thus avoiding a serious overshoot of the controlled quantity.

Therefore, for controlled objects with large inertia and/or hysteresis, the proportional + derivative (PD) controller can improve the dynamic characteristics of the system during the adjustment process.

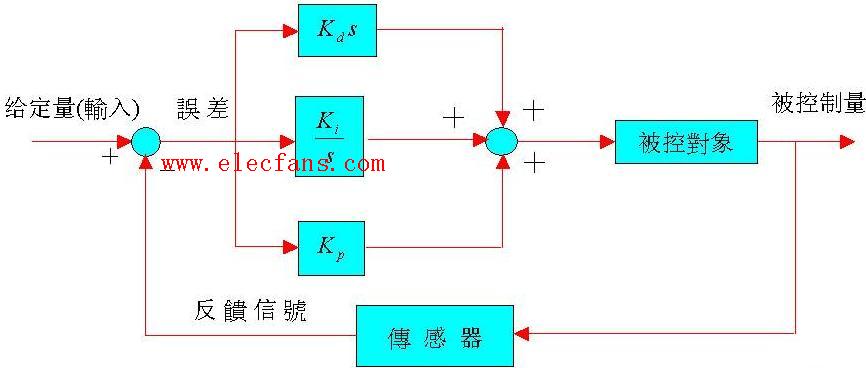
Figure 1.2a Structural diagram of PID control

Today's automatic control technology is based on the concept of feedback. The elements of feedback theory include three components: measurement, comparison, and implementation. The variable of interest is measured, compared with the expected value, and this error correction is used to adjust the response of the control system. The key to this theory and applied automatic control is how to better correct the system after making correct measurements and comparisons. PID (proportional-integral-derivative) controller has been the earliest practical controller for more than 50 years and is still the most widely used industrial controller. The PID controller is simple and easy to understand and does not require precise system models and other prerequisites for use, so it has become the most widely used controller. The PID controller consists of a proportional unit (P), an integral unit (I) and a differential unit (D). Proportional (P) adjustment effect: It responds to the deviation of the system in proportion. Once a deviation occurs in the system, the proportional adjustment immediately produces an adjustment effect to reduce the deviation. A large proportional effect can speed up adjustment and reduce errors, but an excessively large proportion will reduce the stability of the system and even cause system instability. The integral (I) adjustment function is to eliminate the steady-state error of the system and improve the indifference. Because there is an error, the integral adjustment is carried out until there is no difference, the integral adjustment stops, and the integral adjustment output is a constant value. The strength of the integral effect depends on the integration time constant Ti. The smaller Ti, the stronger the integral effect. On the contrary, if Ti is large, the integral effect is weak. Adding integral adjustment can reduce the stability of the system and slow down the dynamic response. The integral effect is often combined with the other two regulation laws to form a PI regulator or PID regulator. Differential (D) adjustment effect: The differential effect reflects the change rate of the system deviation signal. It is foreseeable and can predict the trend of deviation changes. Therefore, it can produce advanced control effects. Before the deviation is formed, it has been eliminated by the differential adjustment effect. Therefore, the dynamic performance of the system can be improved. When the differential time is appropriately selected, overshoot can be reduced and the adjustment time can be reduced. The differential effect amplifies noise interference, so excessive differential adjustment is detrimental to the system's anti-interference. Furthermore, the differential responds to the rate of change, and when there is no change in the input, the output of the differential action is zero. The differential effect cannot be used alone and needs to be combined with the other two adjustment laws to form a PD or PID controller. The relationship between the input e (t) and the output u (t) is: post-supplement , and only three parameters (Kp, Ki and Kd) need to be set during use. In many cases, all three units are not necessarily required, one or two of them can be taken, but the proportional control unit is essential. First of all, PID has a wide range of applications. Although many industrial processes are nonlinear or time-varying, by simplifying them, they can be turned into systems whose basic linear and dynamic characteristics do not change with time, so that PID can be controlled. Secondly, PID parameters are easier to tune. That is, the PID parameters Kp, Ki and Kd can be adjusted in time according to the dynamic characteristics of the process. If the dynamic characteristics of the process change, for example, the dynamic characteristics of the system may change due to changes in load, the PID parameters can be re-tuned. Third, the PID controller has been continuously improved in practice. The following two improvements

Example. In factories, you will always see many loops in manual mode because it is difficult to make the process work
smoothly in "automatic" mode . Due to these shortcomings, industrial control systems using PID are always troubled by issues such as product quality, safety, yield, and energy waste. PID parameter self-tuning was created to deal with the problem of PID parameter tuning. Today, self-tuning or self-tuning PID controllers are a standard in commercial single-loop controllers and distributed control systems. In some cases PID controllers designed for specific systems control well, but they still have some problems that need to be solved: If self-tuning is to be model-based, finding and maintaining a good process model online for re-tuning of PID parameters is More difficult. When working in closed loop, it is required to insert a test signal into the process. This method will cause disturbances, so model-based PID parameter self-tuning is not very good for industrial applications. If self-tuning is based on a control law, it is often difficult to distinguish the effects caused by load disturbances from the effects caused by changes in process dynamics. Therefore, the controller will overshoot under the influence of disturbances and produce an unnecessary adaptive transition. . In addition, since there is no mature stability analysis method for systems based on control laws, there are many problems with whether parameter tuning is reliable. Therefore, many PID controllers with self-tuning parameters often work in automatic tuning mode rather than continuous self-tuning mode. Automatic tuning usually refers to the automatic calculation of PID parameters based on a simple process model determined by the open-loop state. But it is still undeniable that PID also has its inherent shortcomings: PID does not work very well when controlling complex processes that are nonlinear, time-varying, coupled, and have uncertain parameters and structures. The most important thing is that if the PID controller cannot control a complex process, no matter how you adjust the parameters, it will be useless. Despite these shortcomings, PID controllers are the simplest and sometimes the best controllers