Design of N-ary asynchronous counter

An asynchronous counter circuit refers to a circuit whose basic functional unit trigger has a clock input signal that is not together with the trigger. Some are external input pulse signals, and some are outputs of other triggers. This article gives a design scheme for an N-ary asynchronous counter .

1. How to select the clock signal for each trigger

The change of the trigger state must be triggered by a trigger pulse. Therefore, when selecting the clock signal for each trigger, it must be satisfied that the trigger signal arrives at the moment when all the states of the trigger change. At the same time, the number of trigger signals arriving for the unchanged state should be as small as possible. According to the second principle, referring to the design of the binary asynchronous counter, the selection of the clock signal of each trigger starts from the previous one. For example, when selecting the CP3 signal of the Q3 trigger, first check whether the output of Q2 meets the first principle mentioned above. If not, then check the output of Ql, and continue forward until a clock signal that meets the requirements is selected.

2. How to design the simplest form of activation function

Since the selected CP signal corresponds to an unchanged state without the arrival of a pulse, no matter what the input value of the trigger is, the trigger state without a pulse will not change. When designing, this state is regarded as an "irrelevant item", which can make the designed excitation function simpler.

Let's take an 11-base counter as an example. Designing an 11-base counter requires at least 4 triggers, whose states correspond to Q3 Q2 Q1 Q0. The attached table is a simplified state table of the 11-base counter. Two adjacent rows: the previous row is the "current state" of the next row, and the next row is the "next state" of the previous row. According to the attached table, it is relatively easy to complete the first step of the design: select the CP pulse for each trigger (assuming the trigger is a falling edge trigger).

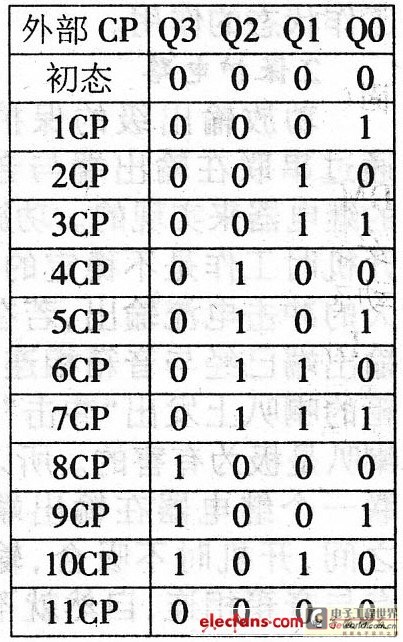
Design of Q3 trigger clock signal CP3: First observe Q2, and find that when the Q3 state changes from "0" to "1", Q2 has a downward jump pulse, but when Q3 changes from "1" to "0", Q2 does not change, so Q2 cannot be used as the clock signal of Q3 trigger; observe the two changes of Q1 and Q3, Q1 has a downward jump pulse, so CP3=Q1.

Design of Q2 trigger clock signal CP2: First observe the two state changes of Ql and Q2 (when the external 4CP is, Q2 changes from "0" to "1"; when 8CP is, Q2 changes from "1" to "0"), both correspond to Q1 having a down-jump trigger, so CP2=Q1.

Design of the clock signal CP1 of the Q1 trigger: When 11CP comes from the outside, Q1 changes from "1" to "0", but Q0 has no corresponding down-jump pulse, so only the external clock signal can be selected as CPI, that is, CP1=CP. CP0=CP of the Q0 trigger.

If the selected trigger is rising edge triggered, just select the Q of the corresponding trigger as the CP signal.

After selecting the clock signal of each trigger, start designing the trigger's excitation function: according to the attached table and the CP pulse signal of the trigger, draw the "next state" Karnaugh map of each trigger, obtain the "next state" equation, and then obtain the excitation function according to the type of selected trigger.

Q3's "next state" equation: As can be seen from the attached table, Q1 has three down-jump triggers as CP3. When the "current states" are 0011, 0111, and 1010, the corresponding "next states" of Q3 are "0", "1", and "0" respectively, and are filled in Figure 1. Since there is no CP pulse trigger in other states, no matter "0" or "1" is filled in the Karnaugh map in Figure 1, the state remains unchanged and can be regarded as "irrelevant terms" to obtain the simplest "next state" equation. In addition, 1011-1111 are real "irrelevant terms". According to Figure 1, Q3n+1=Q2.

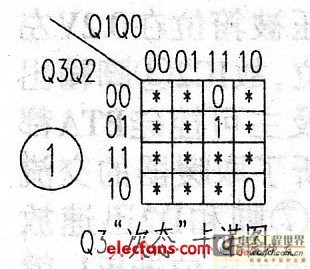
If CP3=CP is selected, a trigger pulse will arrive in each state, so the "next state" Karnaugh map is shown in Figure 2, and the resulting equation is more complicated.

The "next state" equation of Q2: CP2 is also Q1, and there are also 3 down-jump triggers. When the "current states" are 0011, 0111, and 1010, the corresponding "next states" of Q2 are "1", "0", and "0" respectively, and are filled in Figure 3; the other states are the same as Q3. According to Figure 3, Q2n+1=Q3Q2. If CP2=CP is selected, the state equation is also more complicated.

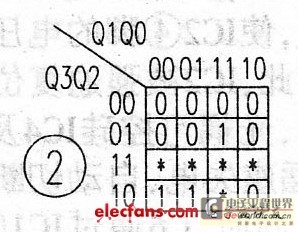
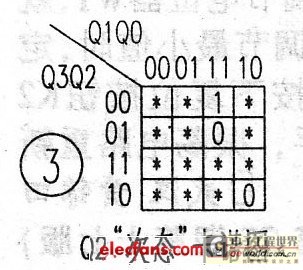
The "sub-state" equation of Q1: CPI=CP, each state has the arrival of a trigger pulse, and the "sub-state" Karnaugh map is shown in Figure 4, Qln+1=Q0Q1+Q3Q0Q1.

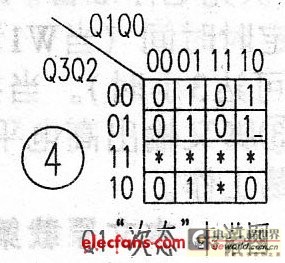
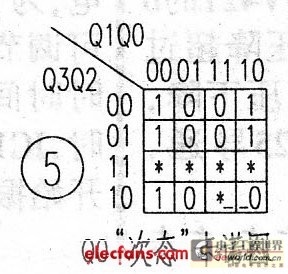
The "sub-state" equation of Q0 is: CP0=CP, and the "sub-state" Karnaugh map is shown in Figure 5, Q0n+1=QlQ0+Q3Q0.

If a JK flip-flop is used, the above "next state" equations are compared with the characteristic equation of the JK flip-flop Qn+1=JQ+KQ, and the driving functions of each flip-flop are obtained: J3=Q2, K3=Q2; J2=Q3, K2=1; J1=Q0, K1=Q3 Q0; JO=Q3 Q1, KO=1.

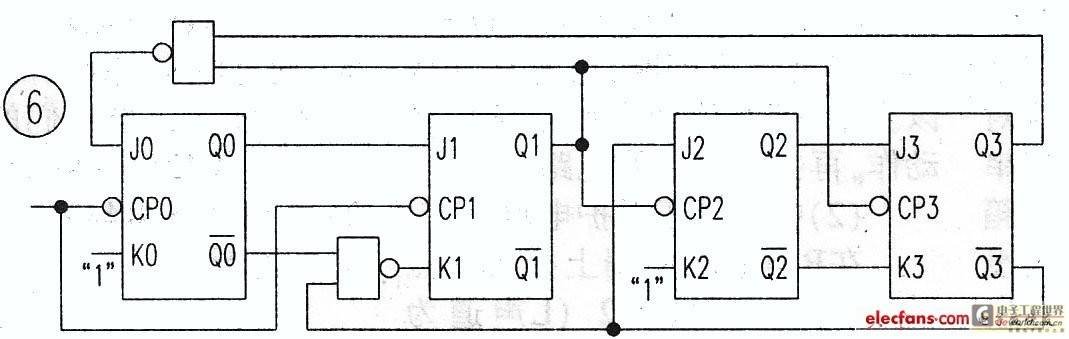
Finally, the circuit was found to have self-starting capability. Draw the logic circuit, see Figure 6.