Introduction

The Kalman filter combines the state estimate of the system at the next moment with the feedback obtained from the measurement to finally obtain a more accurate state estimate (prediction + measurement feedback) at that moment. The Kalman filter KF we generally refer to is for linear systems, and its idea is also applicable to nonlinear systems. Extended from this are EKF, UKF, etc.

Let's start with a simple question to understand the idea of ​​Kalman filtering.

Suppose we want to know the thickness of a coin and have k measurements . In order to estimate the true value, we generally take the average, so the estimated value is

From formula ①, we know that when we have only one measurement value, that is, k = 1, we can only choose to believe the measurement value, and when k —>∞, we can believe the last estimated value. And this estimate is only related to this measurement value and the last estimate, and there is no need to trace back to the previous k-1 measurements.

Where Kk is the Kalman gain. To minimize the estimation error, we minimize the variance , let , and then do the following transformation to get the general form of the Kalman gain. This Kk value has mathematical optimality.

eEST is the estimation error, and eMEA is the measurement error. From formula ②, we know that when eEST ≫eMEA, Kk = 1, which is substituted into formula ① , that is, when the estimation error is relatively large, we choose to believe the measured value. On the contrary, when eEST ≪eMEA, Kk = 0, 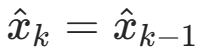, at this time we choose to believe the estimated value

The general steps of Kalman filtering in this case are:

Kalman filter

Consider the system

Where ω is the process noise, which follows the N(0,Q) distribution. υ is the measurement noise, which follows the N(0,R) distribution.

1. Covariance matrix

Represent the variance and covariance through a matrix

variance:

Covariance:

Consider the following third-order covariance matrix

Construct the transition matrix T to find the covariance matrix, which forms the mean value matrix of

For the system represented by formula ③

Since D(X) = E(X ^2^ ) - E ^2^ (X), and E(ω_i) = 0, the covariance matrix can be expressed as follows

At the same time, ω 1 , ω 2 , … , ωn are independent of each other.

Similarly, R = E(υυ ^T^ )

2. Prior estimation

Without considering process error and measurement error, it is calculated by the state space equation

However, in the motor model, ω and θ are not available. We can replace with and obtain from the measurement .

3. Posterior Estimation

Estimation + Measurement Feedback

Let G = KkH, then

4. Kalman Gain

The Kalman gain Kk is the pole of the concave function, so the Kalman filter is both an observer and an optimality estimator.

Let , obey N(0,P) distribution

In order to minimize tr(P), that is, to minimize the variance, let

For the specific derivation process, please refer to the B station UP host DR_CAN, the video link is at the end of the article

Where P^-^ is the prior error

General steps of Kalman filtering

Motor state equation

In the above Lomborg observer, we selected the state vector , but in order to use the Kalman filter to predict ω and θ, we select the state vector , the measurement vector , and modify the back EMF form as follows (the current lags the voltage by 90°, so the back EMF of the α axis is generated by the β axis voltage and is in the opposite direction)

1. State vector

2. Linearization

At this time, the system is a nonlinear system. In order to use Kalman filtering, we must first linearize it and use EKF to estimate the system state.

The non-linear function that is not discretized is used when calculating the prior estimate.

The general step of Kalman calculation above is to make the following corrections to the prior estimate, while the other steps remain unchanged.

Jacobian matrix

then

3. Discretization

So the linearized discrete system matrix

MATALB Simulation

EKF

It can be seen that the θ estimation output of the Kalman filter almost coincides with the actual position. The speed estimation ω is affected by the magnetic flux constant. A larger magnetic flux will lead to a smaller ω estimation. On the contrary, a smaller magnetic flux will lead to a larger ω estimation. It is recommended to use the differential of θ as an estimate of ω.