How Error Vector Magnitude (EVM) Measurements Improve System-Level Performance

How Error Vector Magnitude (EVM) Measurements Improve System-Level Performance

Error Vector Magnitude (EVM) is a widely used system-level performance metric that is defined by many communication standards for compliance testing in applications such as wireless local area networks (WLAN 802.11), mobile communications (4G LTE, 5G), etc. In addition, it is an extremely useful system-level metric that quantifies the combined impact of all potential impairments in the system in a simple and understandable value.

Most RF engineers are trained on a host of RF performance parameters, such as noise figure, third-order intercept point, and signal-to-noise ratio. Understanding the combined impact of these performance parameters on overall system-level performance can be challenging. Rather than evaluating multiple individual performance metrics, EVM reflects an overview of the entire system. In this article, ADI will analyze how lower-level performance parameters affect EVM and examine some real-world examples of using EVM for system-level performance optimization of devices. It will also show how to achieve EVM that is up to 15dB lower than the targets of most communications standards.

What is Error Vector Magnitude?

EVM is a simple metric that quantifies the combined impairments of all signals in a system. It is often defined for devices that use digital modulation and can be represented by an in-phase (I) and quadrature (Q) vector diagram, also known as a constellation diagram, as shown in Figure 1a. In general, EVM is calculated by finding the ideal constellation position for each received signal, as shown in Figure 1b. The EVM value for a device is calculated by calculating the root mean square (rms) of all error vector magnitudes between the received signal's position and its closest ideal constellation position.

An example of an EVM formula that complies with the IEEE 802.11 standard is shown in Equation 1.

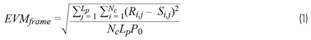
Where: Lp is the number of frames, Nc is the number of carriers, Ri,j is the received signal, and Si,j is the ideal signal position.

Figure 1. (a) Constellation diagram and decision boundary, and (b) error vector between the received signal and the ideal signal position.

EVM is closely related to the bit error rate (BER) of a given system. As received signals move away from a target constellation point, the probability that they fall within the decision boundary of another constellation point increases. This results in a larger BER. An important difference between BER and EVM is that the BER of a transmitted signal is calculated based on the transmitted bit pattern, while EVM is calculated based on the distance between the constellation point closest to the signal and the actual location of the signal. In some cases, a signal may cross a decision boundary and be assigned an incorrect bit pattern. The closer a signal is to another ideal signal location, the better the EVM for that signal may be. Therefore, while EVM and BER are closely related, this relationship may not apply in situations where the signal has extremely high levels of distortion.

Modern communications standards specify minimum acceptable EVM levels based on the characteristics of the transmitted or received signal, such as data rate and bandwidth. Devices that achieve the target EVM level comply with the standard, while devices that do not meet the target EVM level do not comply with the standard. Test and measurement equipment dedicated to communication standard compliance verification typically uses a more stringent EVM specification that may be an order of magnitude lower than the EVM specification established by the standard. This allows the test and measurement equipment to characterize the EVM characteristics of the device under test without significantly distorting the signal.

What are the factors that affect EVM?

As an error metric, EVM is closely related to all error sources within the system. To quantify the impact of all impairments on EVM, the extent to which they distort the received and transmitted signals can be calculated. Below ADI will analyze the impact of several key impairments (such as thermal noise, phase noise, and nonlinearity) on EVM.

White Noise

White noise is present in all RF systems. When noise is the only impairment in the system, the corresponding EVM can be calculated using the following formula:

Where SNR is the signal-to-noise ratio of the system in dB, and PAPR is the peak-to-average power ratio of a given signal in dB. Note that SNR is generally applicable to single-tone signals. If the signal is modulated, the PAPR of the signal needs to be considered. Since the PAPR of a single-tone signal is 3dB, if the waveform has an arbitrary PAPR value, 3dB needs to be subtracted from the SNR value.

For high-speed converters such as analog-to-digital converters (ADCs) and digital-to-analog converters (DACs), Equation 2 can be expressed in terms of noise spectral density (NSD):

Where NSD is the noise spectral density in dBFS/Hz, BW is the signal bandwidth in Hz, PAPR is the peak-to-average power ratio, and Pbackoff is the difference between the signal peak power and the converter full scale. This formula makes it very convenient to directly calculate the expected EVM of a device using the NSD specification, which is commonly used for state-of-the-art high speed converters. Note that high speed converter devices also need to consider quantization noise. Most high speed converters have NSD specifications that also include quantization noise. Therefore, Equation 3 not only represents thermal noise, but also the quantization noise of the high speed converter.

As these two equations highlight, the EVM of a signal is directly related to its total signal bandwidth, peak-to-average ratio, and the thermal noise of the entire system.

How phase noise affects EVM

Phase noise is another form of noise that affects system EVM. It is the random fluctuation of the phase and frequency of the waveform. All nonlinear circuit elements will introduce phase noise. The main sources of phase noise in a given system can be traced back to oscillators such as reference clocks, local oscillators (LOs), and sampling clocks. Multiple oscillators, such as the sampling clock of data converters, local oscillators for frequency conversion, and reference frequencies, will contribute to the overall phase noise of the system.

The performance degradation caused by phase noise is frequency dependent. A typical oscillator generates most of the carrier energy at its fundamental oscillation frequency, the so-called center frequency. A small portion of the signal energy will be spread around this center frequency. The ratio of the signal amplitude in a 1 Hz bandwidth at a specific frequency offset to its amplitude at the center frequency is defined as the phase noise at a specific frequency offset (see Figure 2).

Figure 2. Phase noise.

The phase noise of a system directly affects the EVM of the system. The EVM caused by the phase noise of the system can be calculated by integrating the phase noise over the entire bandwidth. For most modern communication standards using orthogonal frequency domain modulation (OFDM), the phase noise should be integrated starting from approximately 10% of the subcarrier spacing until the total signal bandwidth is reached.

Where L is the single sideband phase noise density, fsc is the subcarrier spacing, and BW is the signal bandwidth.

大多数频率发生器件在低于2GHz的频率下出现低相位噪声，典型的积分抖动水平比标准中定义的EVM限值低几个数量级。但在更高的频率和更宽的信号带宽下，积分相位噪声水平可能会非常大，这可能导致EVM值显著变高。工作频率大于20GHz的毫米波(mmWave)器件通常会发生这种情况。要获得最佳的整体EVM，应计算整个系统的相位噪声，这将在“设计示例”部分详细讨论。

Calculating the impact of nonlinearity on EVM

System-level nonlinearities result in intermodulation products that can be within the signal bandwidth. These intermodulation products can overlap subcarriers, affecting their amplitude and phase. The average error due to these intermodulation terms can be calculated. Let's derive a simple formula to calculate the system EVM caused by third-order intermodulation products.

Figure 3. OFDM intermodulation products

As shown in Figure 3a, a two-tone signal will produce two intermodulation products. The power of the intermodulation products can be calculated by the following formula:

Where Ptone is the power of the test tone, OIP3 is the output third-order intercept point, and Pe is the error signal, which represents the power difference between the fundamental wave and the intermodulation product.

If the OFDM signal has N tones (as shown in Figure 3b), Equation 6 becomes:

Since there are N/2 intermodulation products overlapping at each subcarrier position, the equation can be rewritten as:

The total error including all subcarrier positions is:

Substituting Equation 6 into Equation 8, the EVM can be expressed as follows:

Where PRMS is the RMS average value of the signal and C is a constant that can range from 0dB to 3dB, depending on the modulation scheme. As shown in Equation 11, EVM decreases as the OIP3 of the system increases. This is as expected, as higher OIP3 generally means a more linear system. Additionally, as the RMS power of the signal decreases, EVM decreases as the power of the nonlinear products decreases.

Using the EVM to Optimize System-Level Performance

Typical system-level designs begin with cascade analysis, using low-level performance parameters of building blocks to determine the overall performance of the system built using those blocks. The analytical formulas and tools available to calculate these parameters are well established. However, many engineers do not consider how to properly use cascade analysis tools to design a fully optimized system.

As a system-level performance indicator, EVM provides an important reference for design engineers to optimize system design. Designers can achieve the best system design by simply selecting the optimized EVM root mean square value without considering multiple parameters.