CTSD Precision ADCs – Part 2: Introducing the CTSD Architecture for Signal Chain Designers

This article will introduce continuous-time Σ-Δ (CTSD) ADC technology in a different way than the traditional approach, so that signal chain designers can understand this new and easy-to-use precision ADC technology by imagining it as a simple system connecting certain known components. In Part 1, we focused on the key challenges of existing signal chain designs, which can be greatly simplified by using precision CTSD ADCs to achieve high accuracy while maintaining continuous-time signal integrity. Now the question is what is behind the CTSD architecture that enables it to achieve these advantages?

The traditional approach to explaining CTSD technology concepts is to first understand the fundamentals of a discrete-time sigma-delta (DTSD) modulator loop and then replace the discrete-time loop components with their continuous-time equivalents. While this approach provides insight into the sigma-delta functionality, our goal is to provide a more intuitive understanding of the reasons behind the inherent advantages of precision CTSD ADCs. First, we will outline a step-by-step approach to building a CTSD modulator loop, starting with a common closed-loop inverting amplifier configuration and then combining it with an ADC and DAC. Finally, we will evaluate the basic sigma-delta functionality of the constructed circuit.

Step 1: Review the Closed-Loop Inverting Amplifier Configuration

A key advantage of the CTSD ADC is that it provides an easy-to-drive continuous resistance input, rather than a traditional pre-switched capacitor sampler. The inverting amplifier circuit has a similar input impedance concept and is used as a starting block to build the CTSD modulator loop.

The closed-loop op amp configuration has long been the method of choice for replicating the analog input with high fidelity, and one common op amp configuration, called the inverting amplifier configuration, is shown in Figure 1. 1 One measure of fidelity is the ratio of output to input gain, expressed in ∑-∆ terms and also known as the signal transfer function (STF). Determining the parameters that affect the STF requires circuit analysis.

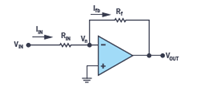
Figure 1. Closed-loop op amp in inverting amplifier configuration.

To solidify our math, let's review the origin of the famous VOUT ⁄VIN. First, we assume that the open-loop gain of op amp A is infinite. With this assumption, the negative input of the op amp, Vn, will be at ground potential. Kirchhoff's laws apply here.

Mapping this to VOUT and VIN, we get the gain or STF as

Next, we abandon the unrealistic infinite gain assumption and redefine the STF under the finite gain A of the op amp. The STF is then expressed as follows:

Here, textbooks usually describe the sensitivity of each parameter RIN, Rf, and A. In this example, we continue to build the CTSD loop.

Step 2: Introducing Discrete Components into the Amplifier

Our ADC signal chain requires a digital version of VIN. Next, we want to introduce digital components into this circuit. Instead of placing a sampling ADC directly on the input signal as is traditionally done, we try a different approach and place a typical ADC device after the amplifier output to obtain digital signal data. However, the output of the ADC cannot be used directly as feedback because it must be an analog voltage. Therefore, we need to place a voltage digital-to-analog converter (DAC) after the ADC, as shown in Figure 2.

Figure 2. Introducing the ADC and DAC in an inverting amplifier configuration

With the ADC and DAC, VOUT still represents VIN, but due to the addition of digital components, there is a quantization error. Therefore, the signal flow from VIN to VOUT does not change. One thing to note here is that in order to keep the loop function symmetrical with respect to 0 V and simplify the mathematical derivation, we choose the reference voltage of the ADC and DAC as follows

Step 3: Introducing the Analog Accumulator - Integrator

Is the closed-loop configuration in Figure 2 stable? Both the ADC and DAC are discrete components operating under the sampling clock MCLK. Designing a latency-free ADC or DAC has always been an unattainable dream for converter experts. Since these loop components are timed, the input is usually sampled on one clock edge and processed on another clock edge. Therefore, the combined output of the ADC and DAC, VOUT (i.e., the feedback in Figure 2), needs to be delayed by 1 clock cycle before it is available.

Does this feedback delay have an effect on stability? Let's look at how VIN is transmitted. For simplicity, we assume that VIN = 1, RIN = 1, Rf = 1, and the gain of op amp A is 100. During the first clock cycle, the input voltage is 1, the DAC output feedback VOUT or VOUTDAC is 0, and it is not available until the next clock edge. When we track the error between the input and output feedback of the amplifier and ADC, we can see that the output has been increasing exponentially, which is technically called the runaway problem.

Table 1. Clock edge sampling

This is because of the effect of the ADC input on the instantaneous error seen by the amplifier; that is, the ADC is determined to have this effect even before feedback is obtained, which is undesirable. If the ADC affects the accumulated average error data so that the error due to the 1 clock cycle delayed feedback reaches the average, the output of the system will be limited.

The integrator is the analog equivalent of an averaging accumulator. The loop gain is still high, but only at low frequencies, or in the frequency bandwidth of interest. This ensures that the ADC does not see any transient errors that could lead to a runaway situation. Therefore, the amplifier in the loop is now changed to an integrator followed by the ADC and DAC, as shown in Figure 3a.

Step 4: Simplify the Feedback Resistor

The target component here is DOUTADC, and we will rearrange the loop components to focus on DOUTADC as the output of the system, as shown in Figure 3b. Next, let's consider the simplification of the DAC and Rf path. To do this, let's take a closer look at the DAC. The role of the DAC is to convert the DIN digital signal into an equivalent analog current or voltage proportional to the reference voltage. To further expand the advantage of the continuity of the reference voltage source, we consider a universal DAC architecture based on a ladder resistor, which has no switching load for the reference voltage source. Let's look at the temperature measuring resistor DAC,2 which converts DIN to a DAC current according to Equation 5.

where VREF = VREFP – VREFM, which is the total reference voltage for the DAC.

► DIN = Digital input in the thermometer code

► Rf = feedback resistor; broken down into each unit element

► N = number of digits

Figure 3. (a) Introducing the integrator into the loop. (b) Rearranging the loop to focus on DOUTADC as the output

Figure 4. General purpose temperature sensing resistor DAC

To obtain a voltage output, an I to V conversion is performed using an operational amplifier in a transimpedance configuration,3 as shown in Figure 4. Therefore,

Returning to the discrete loop of Figure 3b, this VOUTDAC is converted back to current Ifb through the feedback resistor of the inverting amplifier, that is, the signal flow is IDAC → VOUTDA C → Ifb. It can be expressed mathematically as:

From the signal flow and equations above, we can see that converting VOUTDAC to Ifb is a redundant step and can be bypassed. Removing the redundant components and expressing (VREFP – VREFM) as VREF for simplicity, we redraw the loop as shown in Figure 5.

Figure 5. Removing the redundant I-to-V conversion section and feedback resistors.

Voila! We have built a first order Σ-Δ loop! Connect all the known components together i.e. inverting amplifier, ADC and DAC.

Step 5: Understanding Oversampling

At this point we have mastered the construction of the CTSD loop, but we have not yet realized what is unique about this particular loop. First, let’s understand oversampling. ADC data is only useful if there are enough sampled and digitized data points to extract or interpret the analog signal information. The Nyquist criterion suggests that in order to faithfully reconstruct the input signal, the ADC should be sampled at least twice the signal frequency. If we continue to add more data points to this minimum requirement, the interpretation error will be further reduced. Following this line of thought, choosing a sampling frequency in ∑-∆ that is much higher than the recommended Nyquist frequency is called oversampling. Oversampling4 helps reduce the quantization noise in the frequency band of interest by spreading the total noise over a higher frequency range, as shown in Figure 6.

Figure 6. Noise spectral density comparison between Nyquist sampling and oversampling

Step 6: Understanding Noise Shaping

Signal chain designers should not be confused when sigma-delta experts use terms such as noise transfer function (NTF) or noise shaping,4 and our next step will help them gain an intuitive understanding of these terms that are specific to sigma-delta converters. Let’s review the simple inverting amplifier configuration and the error Qe generated at the amplifier output, as shown in Figure 7.

Figure 7. Error generation in an inverting amplifier configuration.

The contribution of this error at the output can be quantified as

From the mathematical formula, we can see that the error Qe is attenuated by the open-loop gain of the amplifier, which again shows the advantage of the closed loop.

This understanding of the benefits of closed-loop can be extended to the quantization error, Qe, of the ADC in the CTSD loop, which is caused by the digitization of the continuous signal at the integrator output, as shown in Figure 8.

Figure 8. Quantization error Qe generated in the ∑-∆ loop

We can now intuitively conclude that this Qe can be attenuated by an integrator. The integrator TF is |HINTEG (f)| = 1/|s × RC| = 1/2πfRC, and its corresponding frequency domain representation is shown in Figure 9. Its curve is equivalent to the curve of a low-pass filter with high gain at low frequencies, and the gain decreases linearly with increasing frequency. Accordingly, the attenuation variation of Qe is similar to the performance of a high-pass filter.