Time Domain Analysis of Control Systems--Transient Response of High-Order Systems

Time Domain Analysis of Control Systems--Transient Response of High-Order Systems

When the system is higher than the second order, it is called a high-order system. Its transfer function can generally be written as follows

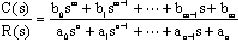
Factoring the above equation, we can write

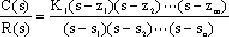
Where si: transfer function pole, i=1, 2,…, n;
zj: transfer function pole, j=1, 2,…, m.

Assume that all zeros and poles of the system are different from each other, and assume that there are real poles and complex poles among the poles, and only real zeros among the zeros. When the input is a unit step function, the image function of its step response is

= + +

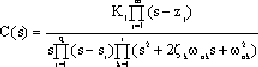
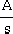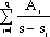Where m is the total number of zeros in the transfer function;
n is the total number of poles in the transfer function, n=q+2r;
q is the number of real poles;
r is the logarithm of the conjugate complex poles.

By solving the original function of the above formula, we can get the unit step response of the high-order system:

c(t) = A + +

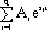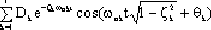
Where Ai =

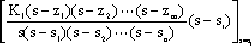
Dk =

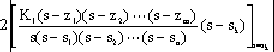
θk=

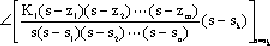
sk=-

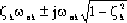
It can be seen that the transient response of a high-order system is a synthesis of the transient response components of the first-order and second-order systems. The following conclusions can be drawn:

1. The decay speed of each component of the transient response of a high-order system is determined by the exponential decay coefficient si. Assuming that the distance between a pair of complex poles of the system and the imaginary axis is 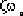, and the distance between another pair of complex poles and the imaginary axis is 5 times that, that is, 5 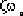, as estimated by formula (3-15), the decay time of the transient component corresponding to the latter is about 1/5 of that of the former. It can be seen that the farther the pole of the system is from the imaginary axis in the left half of the s plane, the faster the corresponding transient component decays.

2. The coefficients Ai and Dk of each component of the transient response of a high-order system are not only related to the position of the poles in the s-plane, but also to the position of the zeros. When a certain pole si is closer to a certain zero zj and farther away from other poles, and is also far away from the origin of the s-plane, the smaller the coefficient Ai of the corresponding component is, the smaller the impact of the transient component is. If a pair of zeros and poles are close to each other, the pole has almost no effect on the transient response. In extreme cases, if a pair of zeros and poles coincide (dipole), the pole has no effect on the transient response. If a certain pole si is far away from the zero point but close to the origin of the S-plane, the corresponding coefficient Ai of the component is relatively large, so the impact of the component on the transient response is greater. Therefore, for components with very small coefficients and transient components with fast attenuation corresponding to poles far away from the imaginary axis, they can often be ignored, so the response of the high-order system can be approximated by the response of the low-order system.

3. If the pole closest to the imaginary axis in a high-order system has a real part smaller than 1/5 of the real parts of other poles, and there is no zero near the pole, then it can be considered that the response of the system is mainly determined by the pole. These poles that play a dominant role in the response of the system are called the dominant poles of the system. The dominant poles of a high-order system are often conjugate complex poles. If a pair of conjugate complex dominant poles can be found, the high-order system can be approximately analyzed as a second-order system, and accordingly, its transient response performance indicators can be approximately estimated as a second-order system.

When designing a high-order system, the concept of dominant poles is often used to select system parameters so that the system has an expected pair of conjugate complex dominant poles. In this way, the system can be designed approximately using the performance indicators of a second-order system. See the following section on system design for details.