|
When analyzing or designing a system, the response characteristics of a second-order system are often considered a benchmark. Although there are almost no second-order systems in practice, but third-order or higher-order systems, they may be approximated by second-order systems, or their responses can be expressed as a combination of first- and second-order system responses. Therefore, the response of the second-order system will be discussed in detail.
The block diagram of a typical second-order system is shown in Figure 3-6. It consists of a non-periodic link and an integral link in series. The transfer function of the system is
make
but
Figure 3-6 Block diagram of a second-order system
|
From the above formula, it is not difficult to obtain the poles of the closed-loop system as
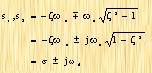
|
(3-12)
|
Where ζ: Damping ratio
ωn: Undamped natural oscillation angular frequency
The unit of oscillation angular frequency ωd is rad/s, but because radians are dimensionless, they only represent the concept of ratio. When studying control systems, it is usually written as s-1, and ωd is often abbreviated as frequency.
From formula (3-12), we can see that the real part of the system pole is σ, which controls whether the transient component of the time response diverges or decays, as well as the rate of change of the transient component over time. When σ>0, the transient response diverges as time increases, and when σ<0, the transient response decays as time increases. Since σ=-ζωn, and ωn cannot be a negative value, it can be seen that when ζ<0, the system transient response will diverge as time increases, and when ζ>0, the system transient response can decay as time increases.
When the damping ratio ζ=1, the system has two real poles, so there is no periodic component in the transient response of the system, and the transient response will decay monotonically over time according to the law of exponential function. At this time, the system is said to be in critical damping.
When ζ=0, the system will have a pair of pure imaginary poles with values of s
1
,s
2
=±jω. At this time, the system is said to be in an undamped state, and the transient response of the system will be a periodic function of constant amplitude, and will be called the undamped natural oscillation angular frequency, or simply the undamped natural oscillation frequency.
When 0<ζ<1, the system has a pair of complex poles with negative real parts, and the transient response of the system will be a periodic function whose amplitude decays exponentially with time. At this time, the system is said to be in an underdamped state.
Figure 3-7 shows the distribution of the corresponding system poles and the step response graph when is different values.
(a) System response when ζ>1 (there are different real roots in the left half plane)
(b) System response when ζ=1 (the left half plane has the same real root)
(c) System response when 0< ζ<1 (there is a conjugate imaginary root with a negative real root in the left half plane)
(d) System response when ζ = 0 (with conjugate imaginary roots on the imaginary axis)
(e) System response when 0>ζ >-1 (there are conjugate imaginary roots with positive real roots in the right half plane)
(f) System response when ζ<-1 (there are different positive real roots in the right half plane)
|
Figure 3-7 System step response graph when pole distribution is different
|
Figure 3-8 illustrates the relationship between the position of the system poles and ζ, ωn, σ, and ωd. For the marked pair of conjugate complex poles, ωn is the radial distance from the pole to the origin of the s plane, σ is the real part of the pole, ωd is the imaginary part of the pole, and the damping ratio ζ is equal to the cosine of the angle between the radial line from the pole to the origin of the s plane and the negative real axis, that is, ζ=cosθ
The damping ratio ζ is an important characteristic parameter of the second-order system.
Figure 3-8 Relationship between system poles and parameters
|
3.5.1 Unit Step Response of a Second-Order System
The unit step response of the second-order system is analyzed below under three conditions: overdamping, critical damping, and negative damping.
(1) Underdamped case (0<ζ<1)
at this time
Where
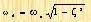 ωd is the damped natural frequency. For a unit step input, C(s) can be written as
ωd is the damped natural frequency. For a unit step input, C(s) can be written as
To find the inverse Laplace transform of the above equation, write the above equation into the following form
Its inverse Laplace transform is
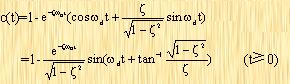
|
(3-13)
|
It can be seen from the above formula that the transient oscillation frequency is the damped natural frequency, which changes with the damping ratio ζ. The error signal of this system is the difference between the input and output, that is,
Obviously, this error signal is a damped sinusoidal oscillation. In steady state or when t=∞, there is no error between the input and output.
If the damping ratio ζ is equal to zero, the response of the system becomes an undamped constant amplitude oscillation. Substituting the value of ζ = 0 into (3-13), we can obtain the response c(t) under zero damping, that is,
As can be seen from the above formula, ωn represents the undamped natural frequency of the system. That is, if the damping coefficient is reduced to zero, the system will vibrate at the frequency ωn. If the linear system has a certain damping, it is impossible to obtain the undamped natural frequency through experiments, but only the damped natural frequency ωd can be obtained, ωd is equal to
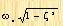 . The damped natural frequency is always lower than the undamped natural frequency ωd. When the ζ value increases, the damped natural frequency ωd will decrease. If ζ increases to greater than 1, the response of the system will become overdamped and no longer oscillate.
. The damped natural frequency is always lower than the undamped natural frequency ωd. When the ζ value increases, the damped natural frequency ωd will decrease. If ζ increases to greater than 1, the response of the system will become overdamped and no longer oscillate.
(2) Critical damping case (ζ=1)
If the two poles of C(s)/R(s) are close to being equal, the system can be approximately regarded as a critically damped system. For a unit step input, R(s)=1/s, so C(s) can be expressed as
The Laplace inverse transform of the above equation is:
(3) Overdamping (ζ>1)
In this case, the two poles of C(s)/R(s) are two unequal negative real numbers. For a unit step input, R(s)=1/s, so C(s) can be written as
Its inverse Laplace transform is
In the formula
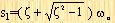 , and
, and
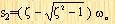 , obviously, the system response c(t) at this time contains two decaying exponential terms.
, obviously, the system response c(t) at this time contains two decaying exponential terms.
When ζ is much larger than 1, one of the two decaying exponential terms decays much faster than the other, so the exponential term that decays faster (corresponding to the exponential term with a smaller time constant) can be ignored. In other words, if -s2 is much closer to the j axis than -s1 (i.e. |s
1
|>>|s
2
|), then -s1 can be ignored in the approximate solution, because the term containing s1 decays much faster than the term containing s2, so the effect of -s1 on the system response is much smaller than the effect of -s2 on the system, so it is reasonable to ignore -s1. Therefore, C(s)/R(s) can be approximately expressed as
This approximate function form is directly obtained based on the following condition: the initial value and final value of the original function C(s)/R(s) and the approximate function are exactly the same.
For the approximate transfer function C(s)/R(s), its unit step response can be expressed as
Its time response c(t) is
In the overdamped case, the unit step response of the second-order system increases monotonically with time and finally approaches the steady-state value when t→∞, so the maximum overshoot is zero. The adjustment time can be estimated by the approximate unit step response. For example, by borrowing the properties of the unit step response of the first-order system, it can be considered that the adjustment time required for the response to reach 95% of the steady-state value is
In engineering, if ζ > 1.5, the above approximation is accurate enough.
3.5.2 Transient response index of second-order system
When the system is underdamped, that is, 0<ζ<1, the calculation formula for the rise time tr, peak time tp, and maximum overshoot Mp of the second-order system step response can be expressed as follows according to formula (3-13).
Rise time tr Let c(t) = 1 and substitute it into equation (3-13) to obtain tr.
or
so
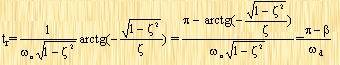
|
(3-14)
|
It can be seen from the above formula that if you want to reduce tr, when ζ is constant, you need to increase ωn. Conversely, if ωn is constant, you need to reduce ζ.
Peak time tp When the first peak appears, the rate of change of the unit step response over time is zero. To find tp, we can take the derivative of equation (3-13) with respect to time t and set it to zero. So we get
From this we can see that:
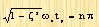
|
n=0, 1, 2, ...
|
When the first peak is reached,
Therefore
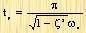
|
(3-15)
|
Maximum overshoot Mp The maximum overshoot occurs when t=tp. Therefore, let t=tp in formula (3-13) and substitute the tp value to get the overshoot expressed as a percentage.
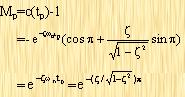
|
(3-16)
|
Adjust the time ts For an underdamped second-order system, the transient response can be obtained from equation (3-13):
The curve
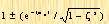 is the envelope of the transient response curve of the system to a unit step input signal. The response curve c(t) is always contained in a pair of envelopes, as shown in Figure 3-9. The time constant of the envelope is 1/(ζωn). Thus, when the 5% allowable error is used, we have
is the envelope of the transient response curve of the system to a unit step input signal. The response curve c(t) is always contained in a pair of envelopes, as shown in Figure 3-9. The time constant of the envelope is 1/(ζωn). Thus, when the 5% allowable error is used, we have
1+
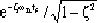 =1.05
=1.05
|
From the above formula, we get
When 0< ζ< 0.8, then
When the 2% tolerance is used, it can be deduced that
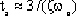
Figure 3-9 Envelope of the unit step time response of a second-order system
|
3.5.3 Impulse Response of Second-Order Systems
When the input signal r(t) is a unit impulse function, the corresponding Laplace transform is 1, that is, R(s)=1. Then the unit impulse response C(s) of the second-order system is
The inverse Laplace transform of this equation is the time domain response solution c(t). When 0≤ζ<1,
c(t) =
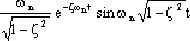 (t≥0)
(t≥0)
|
When ζ=1
c(t) =
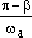 (t≥0)
(t≥0)
|
When ζ>1
c(t) =
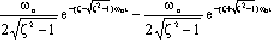 (t≥0)
(t≥0)
|
The unit impulse response curves for different ζ are shown in Figure 3-10. For the case of ζ ≥ 1, the unit impulse response is always positive or zero at t = ∞. In this case, the unit step response of the system must be monotonically increasing.
Since the unit impulse response is the derivative of the unit step response, the time corresponding to the point where the unit impulse response curve first intersects the time axis must be the peak time tp, and the area enclosed by the curve from t=0 to t=tp and the time axis will be equal to 1+Mp (see Figure 3-11), and the algebraic sum of the areas enclosed by the unit impulse response curve and the time axis is 1.
Figure 3-10 Unit pulse response curve
|
Figure 3-11 Determining Mp from the impulse response
|
3-10 In the system shown in the figure, ζ = 0.6, ωn = 5 radians/second. When the system is subjected to a unit step input signal, calculate the rise time tr, peak time tp, maximum overshoot Mp, and adjustment time ts.
Solution: According to the given values of ζ and ωn, we can obtain ωd =
=4 and σ=ζωn =3.
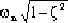
1. Rise time tr
The rise time is:
tr=
=
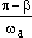
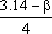
Where β is:
radians
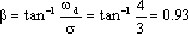
Therefore, the rise time tr can be obtained as: tr =
=
seconds
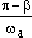
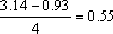
2. Peak time tp
The peak time is:
tp =
=
=0.785 seconds
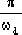
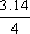
3. Maximum overshoot Mp
The maximum overshoot is:
Mp=
=
=0.095
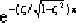
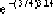
Therefore, the maximum overshoot percentage is 9.5%.
4. Adjust time ts
For the 2% tolerance standard, the adjustment time is:
ts =
=4/3 = 1.33 seconds
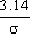
For the 5% tolerance standard, the adjustment time is:
ts =
=3/3 = 1 second
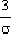
|





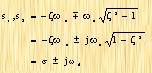








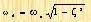 ωd is the damped natural frequency. For a unit step input, C(s) can be written as
ωd is the damped natural frequency. For a unit step input, C(s) can be written as

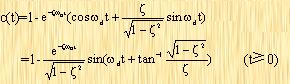

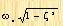 . The damped natural frequency is always lower than the undamped natural frequency ωd. When the ζ value increases, the damped natural frequency ωd will decrease. If ζ increases to greater than 1, the response of the system will become overdamped and no longer oscillate.
. The damped natural frequency is always lower than the undamped natural frequency ωd. When the ζ value increases, the damped natural frequency ωd will decrease. If ζ increases to greater than 1, the response of the system will become overdamped and no longer oscillate.




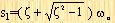 , and
, and
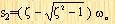 , obviously, the system response c(t) at this time contains two decaying exponential terms.
, obviously, the system response c(t) at this time contains two decaying exponential terms.






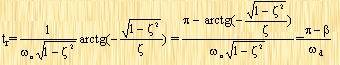

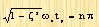

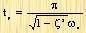
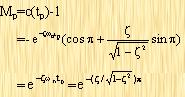

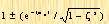 is the envelope of the transient response curve of the system to a unit step input signal. The response curve c(t) is always contained in a pair of envelopes, as shown in Figure 3-9. The time constant of the envelope is 1/(ζωn). Thus, when the 5% allowable error is used, we have
is the envelope of the transient response curve of the system to a unit step input signal. The response curve c(t) is always contained in a pair of envelopes, as shown in Figure 3-9. The time constant of the envelope is 1/(ζωn). Thus, when the 5% allowable error is used, we have


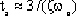


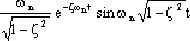 (t≥0)
(t≥0)
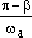 (t≥0)
(t≥0)
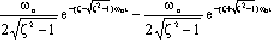 (t≥0)
(t≥0)


 A review of learning-based camera and lidar simulation methods for autonomous driving systems
A review of learning-based camera and lidar simulation methods for autonomous driving systems Visual ModelQ V7
Visual ModelQ V7
















 京公网安备 11010802033920号
京公网安备 11010802033920号