Two expressions of
4.2.1.
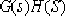
⒈System block diagram: as shown in Figure 4-3.
2.:
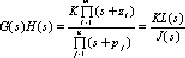
Note:
(1)
 Open-loop amplification factor, gain, transfer coefficient.
Open-loop amplification factor, gain, transfer coefficient.
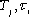 ...time constant.
...time constant.
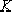 ...transfer coefficient in the form of open-loop zeros and poles.
...transfer coefficient in the form of open-loop zeros and poles.
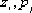 ...negative value of open-loop zeros and poles.
...negative value of open-loop zeros and poles.
(2).
Relationship 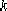 with
with
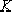 :
:
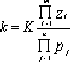
4.2.2 Several expressions of the characteristic equation D(s)=0:
⒈. Several forms of closed-loop transfer function:
⑴.
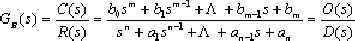
⑵.
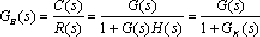
⒉Several forms of "
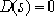 ":
":
⑴.
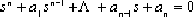
⑵.
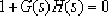
⑶.
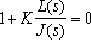
⑷.
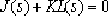
⑸.
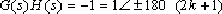 (k=0,1,2,3,……)
(k=0,1,2,3,……)
⑹.
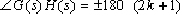
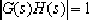
4.2.3 Mathematical basis for drawing root traces:
1. Amplitude angle condition, amplitude condition - amplitude phase condition:
⑴. The so-called phase angle condition (phase angle condition):
①.
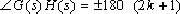 (k=0,1,2,3,……) (4-1)
(k=0,1,2,3,……) (4-1)
②. The argument condition is the fundamental basis for drawing the root trace
- all the points on the root plane that meet the argument condition are the root trace.
③. The argument condition can be used to draw the root trace.
⑵. The so-called amplitude condition:
①.
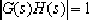 (4-2)
(4-2)
②. Any point on the root trace that satisfies the amplitude condition is the closed-loop pole sb of the corresponding K value, that is,
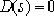 the root of .
the root of .
③. The amplitude condition can be used to determine the K corresponding to sb.
⑶. Differences between the angle condition and the amplitude condition:
① The amplitude condition has nothing to do with K.
② According to the amplitude condition, the change of amplitude corresponds to the change of K.
⑷. Example
Still taking the system shown in Figure 4-1 as an example, the argument condition is used to find the root locus when changing from 0 to +∞, and the amplitude condition is used to determine the K value when the damping ratio ξ of a pair of conjugate complex poles of the closed-loop system is equal to 0.707.
For the given system above, the argument condition is:
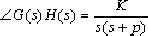
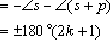 (k=0,1,2,3,...)
(k=0,1,2,3,...)
Its amplitude condition is:
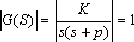
In summary, when drawing the root locus diagram, we only need to apply the argument condition to draw the root locus, and then use the amplitude condition to find the corresponding K value of a point on the root locus. Because the argument and amplitude need to be graphically measured in the process of drawing the root locus on the drawing, the horizontal axis and the vertical axis must be equally divided according to the same scale.
⒉. The steps for drawing the root locus are as follows:
⑴. Draw the open-loop poles on the S plane:
There are two open-loop poles
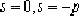 , represented by ×.
, represented by ×.
See Figure 4-4.
⑵. Determine the root locus on the real axis:
If the test point is on the positive real axis, then
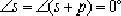 This indicates that the argument condition is not met. Therefore, there is no root locus on the positive real axis. If the test point is selected on the negative real axis,
This indicates that the argument condition is not met. Therefore, there is no root locus on the positive real axis. If the test point is selected on the negative real axis,
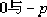 between.
between.
At this time
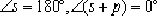 Therefore
Therefore
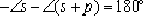
The argument condition is met.
Therefore, on the negative real axis,
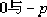 the segment between is part of the root locus.
the segment between is part of the root locus.
If the test point is selected on the negative real axis
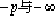 , then
the phase angle condition is obviously not met. Therefore,
the section between
, then
the phase angle condition is obviously not met. Therefore,
the section between
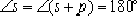 the negative real axis and the
root locus is not part of the root locus.
the negative real axis and the
root locus is not part of the root locus.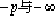
In summary, the root locus on the real axis exists
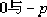 between and on the negative real axis.
between and on the negative real axis.
⑶. Determine the root loci other than the real axis on the S plane:
Take any point on the S plane (see Figure 4-4), let ╱s = Λ1, ╱s+p = Λ2. If it is on the root locus, it should satisfy the argument condition, that is, Λ1+Λ2=180L. Obviously, only
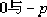 points on the perpendicular bisector of the line segment between the coordinate origins can satisfy the argument condition, so on the S plane, the perpendicular bisector is also part of the root locus.
points on the perpendicular bisector of the line segment between the coordinate origins can satisfy the argument condition, so on the S plane, the perpendicular bisector is also part of the root locus.
To summarize, the root locus obtained and drawn according to the phase angle conditions when K changes from 0→+∞ is exactly the same as the root locus drawn by directly calculating the root value according to the formula in Figure 4-2, and the former is not limited by the order of the system equation and is obviously better than the latter.
⑷. Determine a pair of conjugate complex closed-loop poles with a damping ratio ξ of 0.707:
This pair of closed-loop poles is located on a straight line passing through the origin and with an angle of with the negative real axis
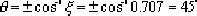 . From the figure, it can be found that when ξ=0.707, this pair of closed-loop poles is
. From the figure, it can be found that when ξ=0.707, this pair of closed-loop poles is
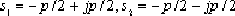
The value corresponding to this pair of poles
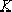 can be determined by the amplitude condition as
can be determined by the amplitude condition as
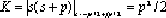
|
 Simulation and Modeling of Chemical Sensors Volume 5 Electro-Optical Sensors Part 1 Photocopy
Simulation and Modeling of Chemical Sensors Volume 5 Electro-Optical Sensors Part 1 Photocopy Signal Integrity and Power Integrity Analysis (Eric Bogatin)
Signal Integrity and Power Integrity Analysis (Eric Bogatin) A Wavelet Introduction to Signal Processing 2nd Edition
A Wavelet Introduction to Signal Processing 2nd Edition Chip Manufacturing: A Practical Tutorial on Semiconductor Process Technology (Sixth Edition)
Chip Manufacturing: A Practical Tutorial on Semiconductor Process Technology (Sixth Edition)


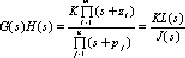
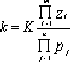

 Simulation and Modeling of Chemical Sensors Volume 5 Electro-Optical Sensors Part 1 Photocopy
Simulation and Modeling of Chemical Sensors Volume 5 Electro-Optical Sensors Part 1 Photocopy













 京公网安备 11010802033920号
京公网安备 11010802033920号