A/D Converter Testing Techniques and Finding Missing Codes in ADCs

A/D Converter Testing Techniques and Finding Missing Codes in ADCs

The quantization noise, dropped bits, harmonic distortion, and other nonlinear distortion characteristics of an A/D converter can be determined by analyzing the spectral components of the converter output.

It is not difficult to determine the degradation of converter performance caused by the above nonlinear characteristics, because these are manifested as some spurious spectral components in the output noise of the A/D converter and the increase of background noise. The traditional measurement method is to add an analog sinusoidal voltage to the input of the A/D converter and then measure the spectrum of the converter's digitized time domain output samples.

FFT can be used to calculate the spectrum of the A/D converter output samples, but in order to improve the sensitivity of the spectrum measurement, the FFT spectrum leakage must be minimized. However, for high-performance A/D converter testing, traditional time domain windowing cannot sufficiently reduce FFT leakage.

The trick to solving FFT leakage is to use an analog sinusoidal input voltage with a frequency that is an integer multiple of the A/D converter clock frequency, as shown in Figure 1(a). This frequency is mfs/N, where m is an integer, fs is the clock frequency (sampling rate), and N is the number of FFT points. When the analog input to an ideal A/D converter is an 8-cycle sampled sine wave from the N = 128 converter output, x(n) in Figure 1(a) is its time domain output.

Figure 1: When the input is a simulated 8fs/128 Hz sinusoid, the analog input to an ideal A/D converter is: (a) output time domain samples; (b) amplitude in dB.

In this example, the input frequency is normalized to the sampling rate fs, which is 8fs/128 Hz. mfs/N defines the analysis frequency, or bin center, of the discrete Fourier transform (DFT). A DFT input sinusoid with a frequency at the bin center will not cause spectral leakage.

In Figure 1(b), the first half of the 128-point FFT of x(n) is plotted on a logarithmic scale. The input frequency is exactly in the center of the frequency bin m = 8, and FFT leakage is effectively reduced. In particular, if the sampling rate is 1 MHz, the analog input frequency to the A/D must be exactly 8(106/128) = 62.5 kHz.

To achieve this, it is necessary to ensure that the analog test signal source is precisely synchronized with the A/D converter clock frequency fs Hz. This is why the A/D converter test process is called coherent sampling.

That is, the analog signal generator and the A/D clock generator that provides fs cannot drift in frequency with respect to each other and must remain coherent (note that from a semantic point of view, quadrature sampling is sometimes referred to as coherent sampling, but quadrature sampling has nothing to do with the A/D converter test process here).

As expected, some values ​​of m are more favorable than others. Note in Figure 1(a) that when m=8, the A/D converter outputs only 9 different amplitude values. These values ​​repeat over and over again. As shown in Figure 2 above, when n=7, there are many more than 9 different A/D output values.

Figure 2: 7-cycle sinusoidal A/D converter output.

Choose m to be an odd prime number

Since it is best to test as many A/D output binary words as possible while keeping the quantization noise sufficiently random, users of the A/D test solution discovered another trick. They found that the repetition of the A/D output words can be minimized when m is chosen to be an odd prime number (3, 5, 7, 11).

Figure 3(a) below shows an extreme example of a nonlinear A/D converter operation, with several discrete outputs dropping the sampled bits into the time domain x(n) with m = 8. Figure 3(b) provides the FFT of this distorted x(n), and when compared to Figure 1(b), it can be seen that the noise floor has increased, due to the nonlinearity of the A/D converter.

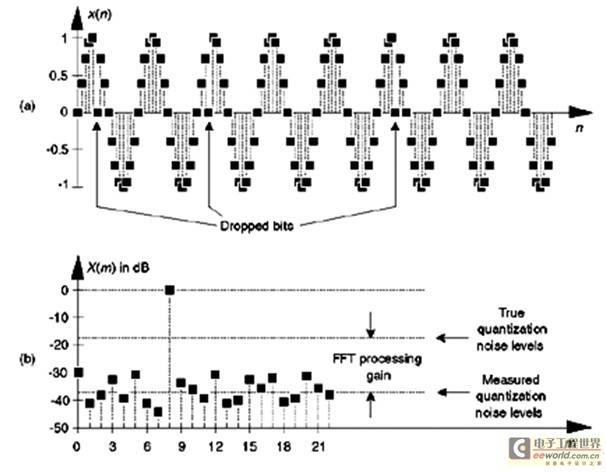
Figure 3: Non-ideal A/D converter output showing several missing bits: (a) time samples; (b) spectral amplitude (in dB).

The quantization noise level of a real A/D converter should be higher than the result measured in Figure 3(b) above. This is because the FFT-related processing gain raises the high-level m=8 spectral component in the background noise.

Therefore, if this A/D test technique is used, the FFT processing gain of 10log10(N/2) shown in Figure 3(b) must be calculated.

In order to fully characterize the dynamic performance of the A/D converter, this test needs to be performed at many different frequencies and amplitudes. Of course, the analog sinusoidal signal applied to the A/D converter must be as pure as possible. Any inherent distortion in the analog signal will show up in the final FFT output and cause A/D nonlinearity problems.

The key is that any input frequency must be mfs/N. Here m is less than N/2 in order to meet the Nyquist sampling criterion, fully utilizing the processing power of the FFT while minimizing frequency leakage.

To quantify the intermodulation distortion of a converter, two analog signals are usually added to the input of the A/D. The intermodulation distortion in turn characterizes the dynamic range of the converter. In this case, both input signals must meet the mfs/N limit. The test configuration is shown in Figure 4.

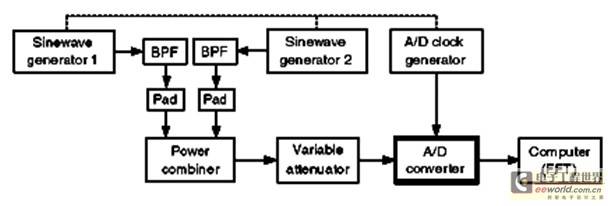
Figure 4: A/D converter hardware test configuration.

When using a low-pass filter (BPF) to improve the purity of the output signal of a sine wave source, caution should be exercised and fixed attenuators (pads) with small attenuation should be used to prevent the two signal sources from interfering with each other. (A 3-dB attenuator is recommended).

A power combiner is usually the reverse application of an analog power divider, and the output of the A/D clock signal generator is also a square wave. The dotted line in Figure 4 above shows that all three signal sources are locked to the same reference frequency source.

Detecting missing code

One problem that affects A/D converters is missing codes. This problem occurs when the converter fails to output a specific binary word (a code). Imagine driving an 8-bit converter with an analog sine wave. The output binary word should be 00100001 (decimal 33), but the actual output is 00100000 (decimal 32), as shown in Figure 5.

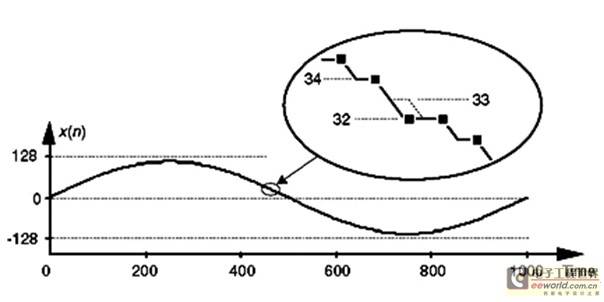
Figure 5: Time domain plot of the missing codes of binary 0010001, decimal 33, for an 8-bit converter.

The binary word representing decimal 33 is a missing code. This tiny nonlinearity is difficult to detect by testing time domain sampling or performing spectrum analysis. Fortunately, there is a simple and reliable way to detect the missing code using histogram analysis.

The statistical histogram analysis test technique simply involves collecting many A/D converter output samples and plotting the number of occurrences of these samples versus their values.

In this statistical histogram, any missing code (such as the missing 33 above) will be displayed as a zero value. In other words, the probability of this binary code representing decimal 33 appearing is zero.