where A1 , A2 , ..., An are input variables.

Combinational logic circuits have the following characteristics:
(1) There is no feedback delay path between the output and input;
(2) The circuit does not contain memory units.
Section 1 Logical Algebra
Logical algebra is also called Boolean algebra. Its basic idea was proposed by British mathematician Boole in 1854. In 1938, Shannon used logical algebra to analyze and simplify switch and relay networks, and was the first to use logical algebra to solve practical problems. After decades of development, logical algebra has become an indispensable mathematical tool for analyzing and designing logic circuits. Logical
algebra provides a method, that is, using binary functions to perform logical operations. In this way
, some logical propositions that seem very complicated when described in words become simple algebraic expressions when using mathematical language. A logical proposition in a logic circuit not only contains the dual meanings of affirmation and negation, but also contains many possible combinations of conditions and results. For example, a 3-input NAND gate has eight possible combinations of input and output states. Using words to describe is both verbose and unclear, using a truth table is clear at a glance, and using the algebraic expression L=ABC is more concise.
Logical algebra has a series of laws and rules, which can be used to process mathematical expressions
to simplify, transform, analyze and design circuits.
1. Basic laws and identities of logical algebra
Commonly used logical algebraic laws and identities table:
|
|||||||||||||||||||||||||||||||
The basic laws in the table are some basic laws of logical operations derived from the three basic operation rules of logical addition, multiplication and negation.
The most effective way to prove the laws listed in the table is to check whether the truth table of the function on the left side of the equation matches that of the function on the right side.
For example, to prove that A+A=A, you can follow the steps below to prove it:
1. Let A=1, then A+A=l+l=l=A;
2. Let A=0, then A+A=0+0=0=A;
Apart from this, there is no other possibility, so A+A=A.
The identity can be proved by other more basic laws. Let's prove the first one, namely,
The proof 
is as follows:
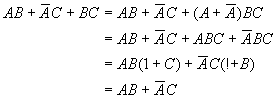
Among all the above laws, the inversion law is of special importance. The inversion law is also called Morgan's law. It is often used to find the non-function of a function or to transform a logical function
.
Example 1:
Prove that the inversion law (Morgan's law) holds
Proof:
Because "when all inputs are 1, the output is 1" is logically equivalent to "when there are 0 inputs, the output is 0", this equivalent relationship can be written as
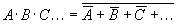



The basic formulas listed in this section reflect logical relationships, not relationships between quantities
. The operation rules of elementary algebra cannot be simply applied to them. For example, the rule of transposition in elementary algebra cannot be used because there is no subtraction and division in logical algebra. This must be noted when using it.
2. Basic Rules of Logical Algebra
1. Substitution rules
In any logical equation, if a variable A on both sides of the equation is replaced by a function, the equation still holds. This rule is called the substitution rule.
For example, in B(A+C)=BA+BC, if all occurrences of A are replaced by the function A+D, the equation still holds, that is, B[(A+D)+C]=B(A+D)+BC=BA+BD+BC
. The substitution rule can expand the scope of application of all basic laws.
2. Inversion rules
According to Morgan's law, when finding the negation of a logic function L
 , you can replace the AND (·) in L with OR (+), or OR (+) with AND (·); then replace the original variable with the non-variable (such as A
, you can replace the AND (·) in L with OR (+), or OR (+) with AND (·); then replace the original variable with the non-variable (such as A
 ), the non-variable with the original variable; and replace 1 with 0, and 0 with 1; then the resulting logic function is
), the non-variable with the original variable; and replace 1 with 0, and 0 with 1; then the resulting logic function is
 . This rule is called the inversion rule.
. This rule is called the inversion rule.
Note that the order of the original expression must be maintained when exchanging, otherwise it is easy to make mistakes.
For example, when finding
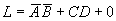 the negation of
the negation of
 , according to the above rule, we can get
, according to the above rule, we can get
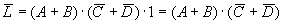 , which cannot be written as
, which cannot be written as
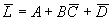 .
.
When using the inversion rule, we must pay attention to two points:
(1) Maintain the original operation priority order, that is, if in the original function expression, AB is operated first, and then other variables are operated, then in the negation expression, AB is still operated first.
(2) The negation sign other than the inverse variable should remain unchanged.
3. Duality rule
L is a logical expression. If we replace the AND (·) in L with OR (+), OR (+) with AND (·); 1 with 0, and 0 with 1, we get a new logical function, which is the dual form of L, denoted as L.
For example,
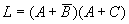 , then
, then
 . When transforming, we still need to pay attention to keeping the order of AND first and OR later in the original formula.
. When transforming, we still need to pay attention to keeping the order of AND first and OR later in the original formula.
The so-called dual rule means that when a certain logical identity is established, its dual form is also established.
Using the dual rule, we can get more operation formulas from known formulas.
For example,
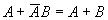 if the absorption law is established, its dual form
if the absorption law is established, its dual form
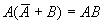 is also established.
is also established.
3. Algebraic transformation and simplification of logical functions
In Chapter 1, we obtained the logical expression of stair lighting control by writing a truth table, which is an exclusive OR function
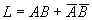 . So, corresponding to the unique truth table, are the logical function expression and the logic circuit that implements it unique? Let's discuss this issue below.
. So, corresponding to the unique truth table, are the logical function expression and the logic circuit that implements it unique? Let's discuss this issue below.
1. Transformation of Logical Functions
Example:
Function
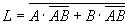 The corresponding logic diagram is shown below. Use the basic laws of logic algebra to transform the above expression.
The corresponding logic diagram is shown below. Use the basic laws of logic algebra to transform the above expression.
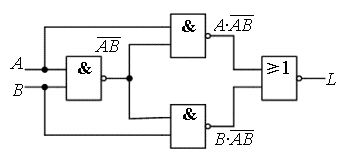
Answer:
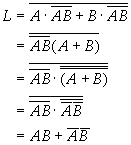
The results show that the circuit shown is also an XNOR gate.
Example:
Find the similarity or the non-function of a function.
Solution:
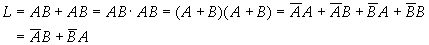
This function is called an XOR function, which means that when the two input variables have different values (one is 0 and the other is 1), the output function value is 1.
In the MOS gate circuit, we have already come into contact with the XOR gate. The above derivation tells us more clearly that the XOR gate and the XNOR gate are each other's negation functions. Therefore, adding another inverter at the output end of the XOR gate circuit can also get the XNOR gate, as shown in the figure below.
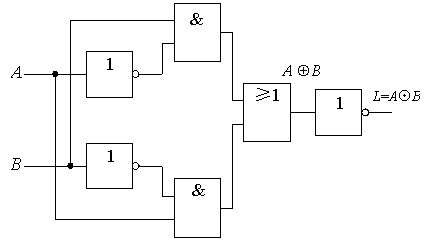
So far, we have learned more than one XOR function, but the truth table of the XOR function is unique. In fact, many more can be listed. From this, we can conclude that for a specific logic problem, the corresponding truth table is unique, but the circuits that implement it are diverse. This brings convenience to circuit design. When we lack a certain logic gate device, we can avoid using this device and use other devices by transforming the function expression. This situation is often encountered in actual work.
2. Simplification of logical functions
According to the logical expression, the corresponding logic diagram can be drawn. However, the logical expression and its corresponding logic diagram directly derived from a certain logical requirement are often not the simplest form, which requires the simplification of the logical expression.
A logical function can have many different logical expressions, such as AND-OR expression, OR-AND expression, AND-NON-AND expression, OR-NON-OR expression, and AND-OR-NON expression.

The above five equations are the simplest expressions of the same function in different forms. The following will focus on the simplification of AND-OR expressions, because AND-OR expressions are easy to write directly from the truth table, and Morgan's law can be used only once to transform the simplest AND-OR expression into a NAND-NAND expression, which can be implemented using a NAND gate circuit.
The simplest AND/OR expression has the following two characteristics:
① The number of AND terms (i.e., product terms) is the least.
② The number of variables in each product term is the least.
Algebraic simplification of logical functions is to use the basic laws and identities of logical algebra to simplify. The following methods are commonly used:
① The method of conjunction

② Absorption method
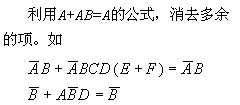
③ Elimination method
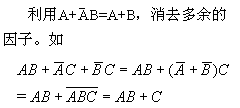
④ Matching method

You need some experience to use the matching method, otherwise the matching will become more and more complicated. Usually, to simplify logical expressions, you need to use the above techniques in combination. Here are a few more examples.
Example 1
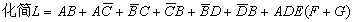
solution:

Example 2
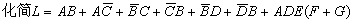


Previous article:Karnaugh Map Simplification Method for Logical Functions
Next article:Capacitor Withstand Voltage and Insulation Resistance
- Popular Resources
- Popular amplifiers
- High signal-to-noise ratio MEMS microphone drives artificial intelligence interaction
- Advantages of using a differential-to-single-ended RF amplifier in a transmit signal chain design
- ON Semiconductor CEO Appears at Munich Electronica Show and Launches Treo Platform
- ON Semiconductor Launches Industry-Leading Analog and Mixed-Signal Platform
- Analog Devices ADAQ7767-1 μModule DAQ Solution for Rapid Development of Precision Data Acquisition Systems Now Available at Mouser
- Domestic high-precision, high-speed ADC chips are on the rise
- Microcontrollers that combine Hi-Fi, intelligence and USB multi-channel features – ushering in a new era of digital audio
- Using capacitive PGA, Naxin Micro launches high-precision multi-channel 24/16-bit Δ-Σ ADC
- Fully Differential Amplifier Provides High Voltage, Low Noise Signals for Precision Data Acquisition Signal Chain
- Innolux's intelligent steer-by-wire solution makes cars smarter and safer
- 8051 MCU - Parity Check
- How to efficiently balance the sensitivity of tactile sensing interfaces
- What should I do if the servo motor shakes? What causes the servo motor to shake quickly?
- 【Brushless Motor】Analysis of three-phase BLDC motor and sharing of two popular development boards
- Midea Industrial Technology's subsidiaries Clou Electronics and Hekang New Energy jointly appeared at the Munich Battery Energy Storage Exhibition and Solar Energy Exhibition
- Guoxin Sichen | Application of ferroelectric memory PB85RS2MC in power battery management, with a capacity of 2M
- Analysis of common faults of frequency converter
- In a head-on competition with Qualcomm, what kind of cockpit products has Intel come up with?
- Dalian Rongke's all-vanadium liquid flow battery energy storage equipment industrialization project has entered the sprint stage before production
- Allegro MicroSystems Introduces Advanced Magnetic and Inductive Position Sensing Solutions at Electronica 2024
- Car key in the left hand, liveness detection radar in the right hand, UWB is imperative for cars!
- After a decade of rapid development, domestic CIS has entered the market
- Aegis Dagger Battery + Thor EM-i Super Hybrid, Geely New Energy has thrown out two "king bombs"
- A brief discussion on functional safety - fault, error, and failure
- In the smart car 2.0 cycle, these core industry chains are facing major opportunities!
- The United States and Japan are developing new batteries. CATL faces challenges? How should China's new energy battery industry respond?
- Murata launches high-precision 6-axis inertial sensor for automobiles
- Ford patents pre-charge alarm to help save costs and respond to emergencies
- New real-time microcontroller system from Texas Instruments enables smarter processing in automotive and industrial applications
- 【Portable Environmental Status Detector】UART Serial Communication
- I am a novice and don't quite understand the dual-channel PWM code with dead zone. I hope you can give me some advice. I would be very grateful. Thank you!!!
- Regarding the relationship between BlueNRG-1 ADC sampling and battery power
- C6000 Timer Application (Part 2)
- Common options for optimizing compilation of TMS320C66x
- Evaluation Weekly Report 20220523: National Technology's low-power series N32L43x is online, and the last two days of RISC-V Linux Starlight Board
- What effects do different packages have on chip resistors and capacitors?
- [Free White Paper Download] Schneider Electric helps Sunny Optical to provide 24/7 uninterrupted power supply
- A 17-year-old boy dropped out of elementary school after three years of school and was sentenced to four years in prison for attacking an airline company's system! He claimed that his girlfriend was pregnant during the epidemic and he was under great pressure
- Peking University and Huazhong University established chip academy

 OPA650N/3K
OPA650N/3K











 京公网安备 11010802033920号
京公网安备 11010802033920号