Fourier Series Decomposition of Non-Sinusoidal Periodic Signals

The analysis and calculation methods of DC circuits and sinusoidal AC circuits have been introduced in detail in the previous chapters. When the excitation source of the circuit is a DC or sinusoidal AC power supply, the above methods can be used to analyze and calculate the circuit. However, in actual electrical systems, non-sinusoidal excitation source problems are often encountered. For example, the electromotive force generated by the AC generator of the power system has a waveform that is not an ideal sinusoidal curve, but a periodic waveform close to a sine wave. Even for a sinusoidal excitation source circuit, if there are nonlinear devices in the circuit, a non-sinusoidal response will be generated. In electronic communication engineering, most of the electrical signals encountered are non-sinusoidal quantities, such as common square waves, triangle waves, pulse waves, etc. Some electrical signals are even non-periodic.

For linear circuits, periodic non-sinusoidal signals can be decomposed into a series of sinusoidal components of different frequencies using Fourier series expansion, and then the sinusoidal AC circuit phasor analysis method is used to calculate the circuit under the action of sinusoidal quantities of different frequencies separately, and then the superposition theorem of linear circuits is used to superimpose the components to obtain the response under the excitation of non-sinusoidal periodic signals. This analysis method of decomposing non-sinusoidal excitation into a series of sinusoidal quantities of different frequencies is called harmonic analysis.

Assume the period of the periodic function is T , then:

( k is an arbitrary integer)

If the function satisfies the Dirichlet condition, then it can be decomposed into a Fourier series. The periodic functions involved in general electrical technology usually satisfy the Dirichlet condition and can be expanded into a Fourier series. This problem will be ignored in the following discussion.

For the above periodic function , it can be expressed as a Fourier series:

(6-1-1)

or (6-1-2)

In the formula, is called the fundamental angular frequency; the coefficients in the two formulas have a relationship:

or (6-1-3)

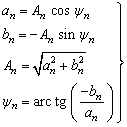
Except for the first term, each term in the expansion is a sinusoidal quantity of different frequencies, which is called the DC component (constant component) of the periodic function. The second term is called the fundamental component, the fundamental angular frequency , and its change period is the same as the original function period. The remaining terms ( terms) are collectively called high-order harmonics. The frequency of the high-order harmonic component is an integer multiple of the fundamental frequency. When is called the second harmonic, when is called the third harmonic, and so on. is the initial phase angle of the nth harmonic .

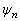
When is known, the coefficients of each harmonic component in the Fourier series expression can be obtained by the following formula:

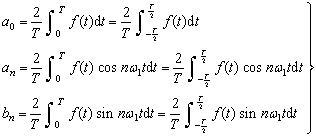(6-1-4)

The following is a specific example to perform Fourier decomposition.

Example 6-1-1 Figure 6-1-1 shows a symmetrical square wave voltage, which can be expressed as:

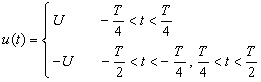
Find the Fourier series expansion of this signal.

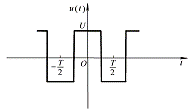
Figure 6-1-1

Solution: According to the Fourier series coefficient derivation formula, we can get

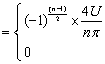
From this, the Fourier series expansion of the desired signal is obtained as

In actual engineering calculations, since the Fourier series expansion is an infinite series, the number of terms to be taken should be determined based on the convergence of the series expansion, the circuit frequency characteristics and the accuracy requirements. Generally, only the first few main harmonic components are needed. For example, for the Fourier series expression of the above square wave expansion, when different numbers of terms are taken to synthesize, the synthesized waveform is shown in Figure 6-1-2. As can be seen from the figure, when the number of harmonic terms is more, the synthesized waveform is closer to the original ideal square wave, and the deviation from the original waveform is smaller.

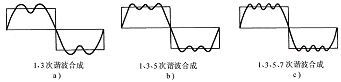
Figure 6-1-2

When some non-sinusoidal periodic signals are expanded, the change of coefficients in the expansion can be determined according to the symmetry of the function. If the function is an even function, , the waveform is symmetrical to the Y axis (see Figure 6-1-3a), then there is no harmonic in its Fourier series expansion , that is, , and this item does not need to be calculated. If the function is an odd function, that is , , the waveform is symmetrical to the origin (see Figure 6-1-3b), and its Fourier series does not contain harmonics and DC components, that is , . If the function satisfies , that is, the waveform is moved half a cycle and is symmetrical to the original waveform on the X axis (see Figure 6-1-3c), then its Fourier series expansion does not contain even harmonic components, that is, . For a detailed discussion of Fourier series, please refer to relevant books.

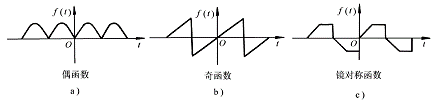
Figure 6-1-3

In addition to being expressed in the above trigonometric form of Fourier series expansion, non-sinusoidal periodic signals can also be expressed in the form of exponential Fourier series expansion. Known functions can be expanded into Fourier series

Using Euler's formula

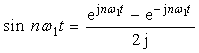
We can get:

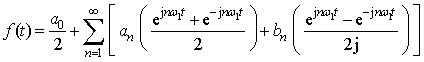
Because for variable n is an odd function, we have:

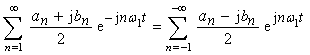
At the same time , when , the terms in the expression can be expressed uniformly as:

(6-1-5)

The above formula is the expression of the Fourier series complex exponential form, which expresses a periodic signal as a series of complex exponential functions with as the exponent, where:

(6-1-6)

The coefficients a _n and b _n are consistent with the coefficients in the Fourier trigonometric expansion. They can be directly calculated by the following formula:

or (6-1-8)

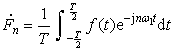
is a function, which represents all the information of each harmonic component in the signal. The modulus of is half of the amplitude of the corresponding harmonic component, and the phase angle of (when n is positive) is the initial phase angle of the corresponding harmonic component. It is a frequency domain expression of a known signal, which is completely equivalent to the time domain expression of the signal. It is called the spectrum function of a given signal. The relationship between the amplitude and the change of is called the amplitude spectrum, and the relationship between the phase and the change of is called the phase spectrum. Due to the coefficient , , the amplitude spectrum is an even function, while the phase spectrum is an odd function. The amplitude and phase of each harmonic contained in the signal can be intuitively represented by the amplitude-frequency characteristic and the phase-frequency characteristic diagram.

Example 6-1-2 The periodic pulse signal is shown in Figure 6-1-4a. Find the spectrum function of the signal and draw the amplitude spectrum and phase spectrum diagrams.

Solution: From the waveform diagram we can see that:

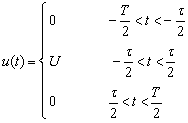
The spectrum function is:

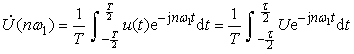
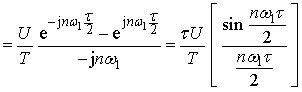(6-1-9)

If , then we can get:

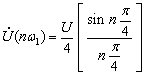
The above formula can be used to produce the amplitude spectrum and phase spectrum, as shown in Figure 6-1-4b and c.

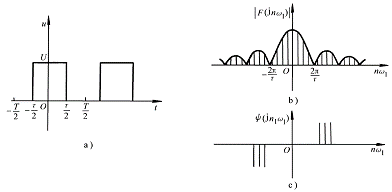
Figure 6-1-4

From the amplitude spectrum diagram, we can see that the spectrum of a periodic signal is composed of a series of discrete spectral lines, all of which appear at frequencies that are integer multiples of the fundamental frequency. This spectrum of a periodic signal is called a discrete spectrum.

From the spectrum function expression, it can be seen that when the pulse repetition period increases, the fundamental frequency will decrease, the interval between the spectrum lines will decrease, and the amplitude will also decrease. When T increases infinitely, the spectrum lines will tend to be infinitely dense, that is, from discrete to continuous, while the amplitude tends to be infinitely small. At this time, the periodic signal has also been transformed into a non-periodic signal.