Research on ISR Method of Direct Torque Control of Asynchronous Motor

1 Introduction

At present, vector control (VC) and direct torque control (DTC) have been recognized as high-performance AC variable frequency speed regulation technologies. The vector control system adopts rotor flux orientation to achieve the decoupling of the stator current torque component and the flux component. The speed and flux regulators (usually PI regulators) can be designed separately according to linear theory to implement continuous control, thereby obtaining a wider speed regulation range, but the system is easily affected by the change of rotor parameters. The direct torque control system abandons the more complex rotating coordinate transformation, directly calculates the electromagnetic torque and stator flux in the stator stationary coordinate system, and uses double-position bang-bang control to adjust the torque and flux. It is less affected by motor parameters and has a fast torque response. However, since bang-bang control itself belongs to P control, torque pulsation is inevitable, affecting the low-speed performance of the system. The ISR (Indirekte Selbst Regelung) control strategy introduced in this paper can effectively reduce the torque pulsation in direct torque control, and has good low-speed performance and dynamic and static characteristics.

2 Dynamic model of asynchronous motor

The voltage equation and electromagnetic torque equation of the asynchronous motor in the stator two-phase stationary coordinate system (α, β) can be expressed as:

uαs=rsiαs+pψαs (1)

uβs=rsiβs+pψβs (2)

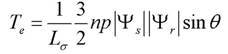(3)
Where: uαs, uβs, iαs, iβs, ψαs, ψβs are the α and β axis components of the stator side voltage, current and flux in the α and β coordinate systems respectively: rs is the stator resistance; np is the number of motor pole pairs; p is the differential operator; is the motor leakage inductance as a constant; θ is the angle between the stator flux and the rotor flux.

From equations (1) and (2), we can get that the stator flux in the stator two-phase stationary coordinate system can be expressed as:

(4)
(5)

The main circuit diagram of direct torque control is shown in Figure 1.



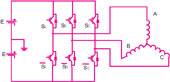
Figure 1 Main circuit diagram of direct torque control

The 8 switching states of the inverter correspond to 8 sets of voltage vectors, as shown in Table 1 [1].

Table 1 Voltage vector table



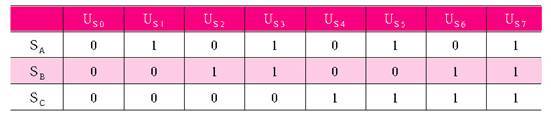
Table 2 Inverter voltage vector selection table



In order to facilitate the control of stator flux and electromagnetic torque, we divide the flux space vector into 6 equal areas. The division principle is:

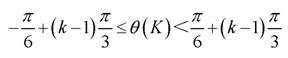(6)

k is the sector number, k=1,2,3,4,5,6, as shown in Figure 2. In each sector, different voltage vectors are selected for different conditions of flux and torque. Figure 3 is a bang-bang control scheme.



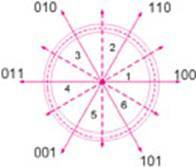
Figure 2 Sector and voltage vector diagram



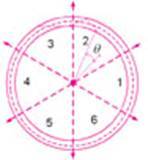
Figure 3 bang-bang control

3 Traditional bang-bang hysteresis control strategy

3.1 Control of stator flux

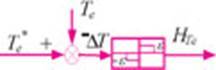
The calculation model of stator flux can be constructed by equations (4) and (5), so as to obtain the actual value of stator flux ψs. Figure 4 is the stator flux hysteresis control diagram. Figure 5 is the electromagnetic torque hysteresis control diagram. Figure 4 Stator flux hysteresis control diagram Figure



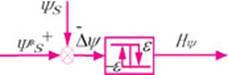
5



Electromagnetic torque hysteresis control diagram


The input of the flux hysteresis is the difference between the flux set value ψs* and the actual flux value ψs, and the output is the flux switching signal hψ, ±ε is the hysteresis width. The flux error is defined as: δψ=ψs*-ψs, then the control method of the flux regulator is as follows:

(1) When δψ≥ε, hψ=1, at this time, the voltage vector is selected to increase |ψs|.

(2) When δψ≤-ε, hψ=-1, at this time, the voltage vector is selected to reduce |ψs|.

3.2 Control of electromagnetic torque

The input of the torque regulator is the difference between the torque given value te* and the actual torque value te, and the output switching signal hte is the tolerance width ε. The regulator adopts a discrete three-point adjustment method, and the torque error is:

δt= te*- te.

The control law of the torque regulator is as follows:

when δt≥ε, hte=1;
when |δt|≤ε, hte=0;
when δt＜-ε, hte=-1;

after obtaining the output signals of flux and torque, we can select the corresponding stator voltage vector according to Table 2.

When the stator flux and electromagnetic torque reach the upper and lower limits of the hysteresis loop, the controller adjusts the stator voltage vector so that the flux and torque meet the set requirements as shown in Figure 3.

4 New control scheme based on pi regulator

For equations (4) and (5), we can approximate by ignoring the stator resistance:
(7)
(8)
By transforming (7) and (8), we can obtain:
(9)
We can see that when the stator resistance voltage drop is ignored, the change of the stator flux per unit time is the voltage vector applied to the stator side, that is, the trajectory of the flux can be determined by the stator voltage vector per unit time [2][3], as shown in Figure 6.

In hysteresis control, the regulator will only adjust when the torque or flux reaches the set hysteresis width. In the new scheme, the regulation of the stator flux and electromagnetic torque is performed per unit sampling time, which makes the regulation more precise and reduces the torque pulsation. In addition, since the regulation of the stator side voltage vector is performed per unit time, the switching frequency of the inverter is constant, which solves the disadvantage of the non-fixed switching frequency of traditional DTC control. The structure of replacing hysteresis control with pi regulator is shown in Figure 7.



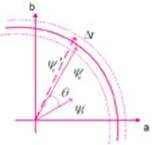
Figure 6 Flux change per unit time



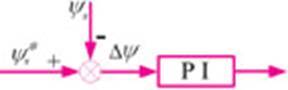
Figure 7 Stator flux pi regulator control
The specific control strategy of flux regulation is: the calculated value of flux is compared with the given value. If the pi output is greater than zero, hψ=1 is set. At this time, the stator flux needs to be increased until the pi output is zero. When the pi output is less than zero, hψ=-1 is set. At this time, the flux needs to be reduced until the pi output is zero. Similarly, the calculated value of torque is compared with the given value. For torque regulation, if the pi output is greater than zero, hte=1 is set. At this time, the electromagnetic torque needs to be increased until the pi output is zero. When the pi output is less than zero, hte=-1 is set. At this time, the flux needs to be reduced until the pi output is zero.

The specific implementation in matlab is shown in Figure 8. The torque regulator has the same structure as the flux regulator. Figure 8 Comparison and analysis of simulation waveforms



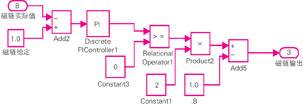
of flux regulator 5 in matlab Matlab simulation comparison of direct torque bang-bang control and pi control of asynchronous motors. Under the same sampling step, the torque change of the control process is shown in Figure 9. The motor first reaches the set speed with the maximum torque and then stabilizes. In the comparison between pi control and bang-bang control, we can clearly see that the torque pulsation of pi control is much smoother than that of bang-bang control, as shown in Figure 10. Figure 9 Torque waveform of asynchronous motor direct torque control Figure 10 Enlarged view of torque waveform of bang-bang control and pi control From the speed response curve in Figure 11, it takes 5ms for the speed to increase from 10rad/s to 20rad/s, indicating that the system has good dynamic and static characteristics. From Figure 12 (a) and Figure 12 (b), we can see that the current curve based on pi control is much smoother than the current curve based on bang-bang control, which shows that pi control is superior to hysteresis control not only in torque control but also in current. Figure 11 Speed ​​response curve of asynchronous motor direct torque control Figure 12 (a) Current curve of pi control Figure 12 (b) Current curve of bang-bang control 6 Conclusion When the system is unloaded, the use of pi regulator instead of bang-bang hysteresis controller can effectively reduce the torque pulsation in the direct torque control scheme, effectively suppress current harmonics, have good low-speed performance and dynamic and static characteristics, facilitate digital implementation, and greatly improve the direct torque control performance.