How to calculate oscilloscope bandwidth?

Bandwidth is a basic indicator of an oscilloscope. It is usually determined by the bandwidth of the measured signal. The following formula can be used as a reference:

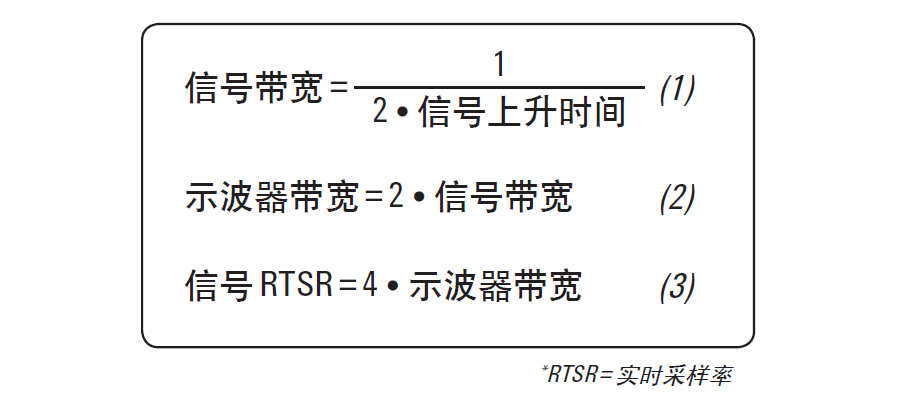
1. Signal bandwidth = 0.5/signal rise time
2. Oscilloscope bandwidth = 2x signal bandwidth

In addition to bandwidth, there are other basic indicators to consider. For example: How much bandwidth do you need? How many channels do you need? What is your required sampling rate? How much memory depth do you need? What display functions do you need? What trigger functions do you need? What is the best way to detect signals? ... Today we will answer them one by one.

1. How much bandwidth do you need for your oscilloscope?

Bandwidth is the most important specification for an oscilloscope because it determines the range of signals that can be displayed without distortion and can be accurately measured, and it also largely determines the price that users have to pay. When deciding on bandwidth, you must balance your current limited budget with the time you will use the oscilloscope in your lab.

To ensure that the oscilloscope has enough bandwidth for your application, you must consider the bandwidth of the signal that the oscilloscope will be displaying. In current digital technology, the system clock is usually the highest frequency signal that an oscilloscope can possibly display. The bandwidth of the oscilloscope should be at least three times higher than this frequency in order to properly display the shape of this signal.

Another signal characteristic that determines the bandwidth required for an oscilloscope is the rise time of the signal. Since you are probably looking at more than a pure sine wave, the signal will contain harmonics at frequencies above the fundamental frequency of the signal. For example, if you are looking at a square wave, the signal will contain frequencies at least 10 times higher than the fundamental frequency of the signal. If you do not ensure the appropriate oscilloscope bandwidth when looking at a square wave, you will see rounded edges on the oscilloscope display instead of the sharp, fast edges you expect. This will in turn affect the accuracy of your measurements.

Fortunately, there are three very simple formulas that can help you determine the appropriate oscilloscope bandwidth based on your signal characteristics:

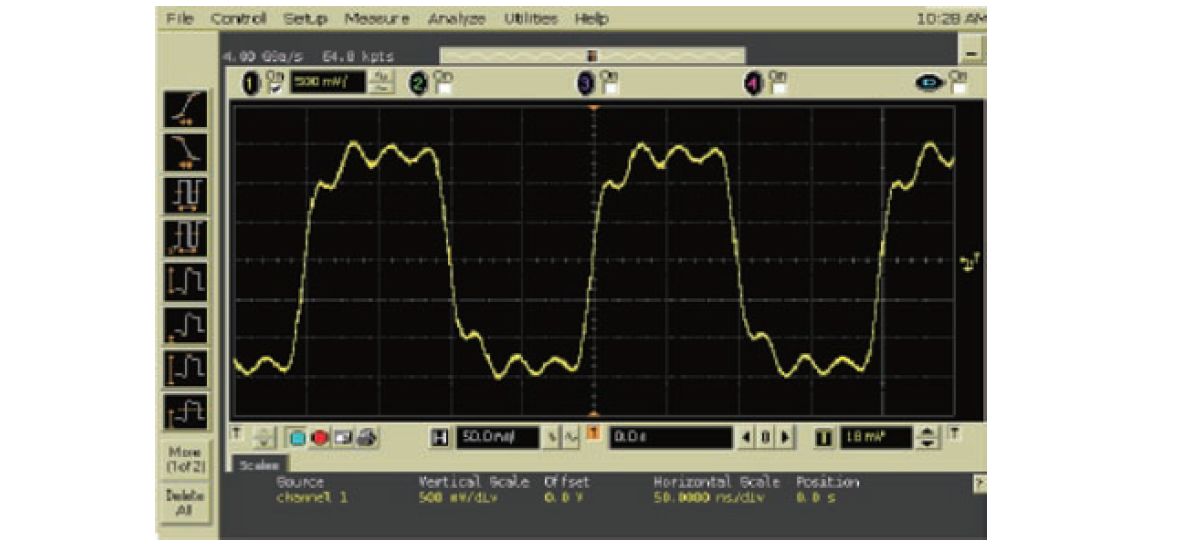
1 GHz Oscilloscope

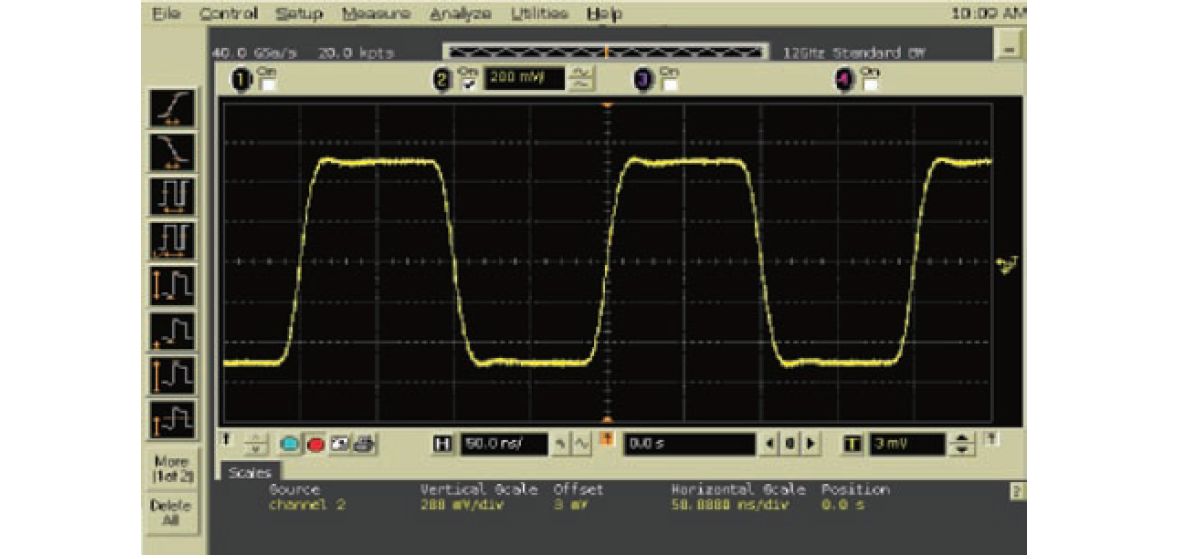
12 GHz Oscilloscope

Figure 1: The same square wave displayed on oscilloscopes with different bandwidths

2. How many channels does your oscilloscope need?

At first glance, the number of channels seems to be a simple question. After all, don't all oscilloscopes come with two or four channels? Nothing more! Digital signals are increasingly common in today's designs, and traditional 2- or 4-channel oscilloscopes don't always provide the number of channels you need. If you've ever been in this situation, you know the pain of building external triggering hardware circuits or writing dedicated software to find multi-channel activity of interest.

As the digital world continues to grow, a new class of oscilloscopes has expanded its reach in digital and embedded debugging applications. In addition to the 2 or 4 channels of a traditional oscilloscope, a mixed signal oscilloscope (commonly referred to as an MSO) provides an additional 16 embedded logic timing channels. As a result, this full-featured oscilloscope provides up to 20 time-correlated triggering, acquisition, and viewing channels.

We will use a common SDRAM application as an example to show how to use a mixed signal oscilloscope for daily debugging. To isolate an SDRAM write cycle, you must trigger on a combination of five different signals: RAS, CAS, WE, CS, and clock. A 4-channel oscilloscope alone is not sufficient to meet this basic measurement requirement.

As shown in Figure 2, the 16 logic timing channels are used to set up the system to trigger on RAS high, CAS low, WE high, and CS. Oscilloscope channel 1 is used to view and trigger on the rising edge of the clock. Unlike a combined logic analyzer and oscilloscope solution, where the logic analyzer can only cross-trigger the oscilloscope (and vice versa), a mixed signal oscilloscope allows full bandwidth triggering on both the oscilloscope and logic timing channels.

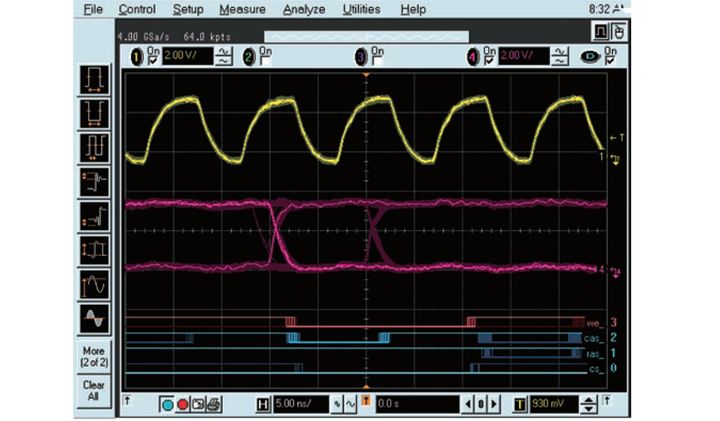
Figure 2: 6-channel measurement: RAS, CAS, WE, CS, and CLK data lines during write triggering.

3. What is the sampling rate of the oscilloscope you require?

As mentioned above, sampling rate is a very important indicator when evaluating an oscilloscope. Why? Many oscilloscopes on the market now use multiple ADCs (analog-to-digital converters) to implement sampling. This can indeed allow a single slower ADC to achieve high-speed sampling. However, the problem faced by this implementation method is that there may be sampling distortion. For example, if you input a sine wave into an oscilloscope, you may find the following waveform. This is caused by sampling distortion.

Recall from the third formula that the oscilloscope's sample rate should be at least four times the oscilloscope's bandwidth. When the oscilloscope uses some form of digital reconstruction (such as sin(x)/x interpolation), it is best to use at least 4 as the multiplier between the sample rate and bandwidth. If the oscilloscope does not use digital reconstruction, then this factor should be 10. Since most oscilloscopes use some form of digital reconstruction, a factor of 4 should be sufficient.

For example, a 12 GHz oscilloscope using sin(x)/x interpolation technology requires a minimum sampling rate of 4 x (12 GHz) or 48 GSa/s per channel to support the full 12 GHz bandwidth on each channel. Some 12 GHz oscilloscopes claim a maximum sampling rate of 64 GSa/s, but do not specify that the 64 GSa/s sampling rate is only for one channel. Such oscilloscopes actually have a sampling rate of only 16 GSa/s per channel, which is not enough to support 12 GHz bandwidth on several channels.

Another way to think about sampling rate is to determine the desired resolution between acquisition points. Sampling rate is the inverse of resolution. Assuming you want 1 ns resolution between acquisition points, the sampling rate that will provide this resolution is 1/(1 ns) = 1 GSa/s.

In summary, make sure the oscilloscope you are looking at has a single-chip ADC sampling that provides sufficient per-channel sampling rate for all channels that may be used simultaneously, so that each channel can support the rated bandwidth of the oscilloscope.

4. How much memory depth is required?

As mentioned previously, bandwidth and sampling rate are closely related. Memory depth is also closely related to sampling rate. The analog-to-digital converter digitizes the input waveform and stores the resulting data in the oscilloscope's high-speed memory. An important factor in selecting an oscilloscope is understanding how the oscilloscope uses the stored information.

Memory technology enables users to capture acquisition data, zoom in to see more details, or perform math, measurements, and post-processing functions on acquired data.

Many people believe that the maximum sample rate specification for an oscilloscope applies to all timebase settings. This is an ideal, but it comes at the expense of potentially requiring very large memory, which greatly increases the price of the oscilloscope. In reality, all oscilloscopes must reduce their sample rate as people set the timebase to a wider and wider range, due to limited memory depth. The deeper the memory of an oscilloscope, the more time it can capture at the maximum sample rate. You need to look at the model of oscilloscope you might buy to understand how the timebase setting affects its sample rate.

The depth of memory you need depends on how long you want to display and the sample rate you want to maintain. If you want to view a longer period of time with higher resolution between acquisition points, you need to use deep memory. You can tell how much memory you need with a simple formula that takes into account the time interval and the sample rate:

If you want to zoom in on a waveform and take a closer look, you need to ensure a high sampling rate at all time settings to prevent signal aliasing while providing detailed information of the waveform.

Once you have determined the memory depth, you must also examine how the oscilloscope operates when using the deepest memory setting. Oscilloscopes with traditional deep memory architectures are slow to respond, which can negatively impact productivity. Because of the slow response, oscilloscope manufacturers typically relegate deep memory to a dedicated mode, where engineers typically only use deep memory when they absolutely must. Although oscilloscope manufacturers have made great strides in deep memory architectures over the years, some deep memory architectures are still slow and time-consuming to operate. Before purchasing an oscilloscope, be sure to evaluate the oscilloscope's responsiveness at its deepest memory setting.

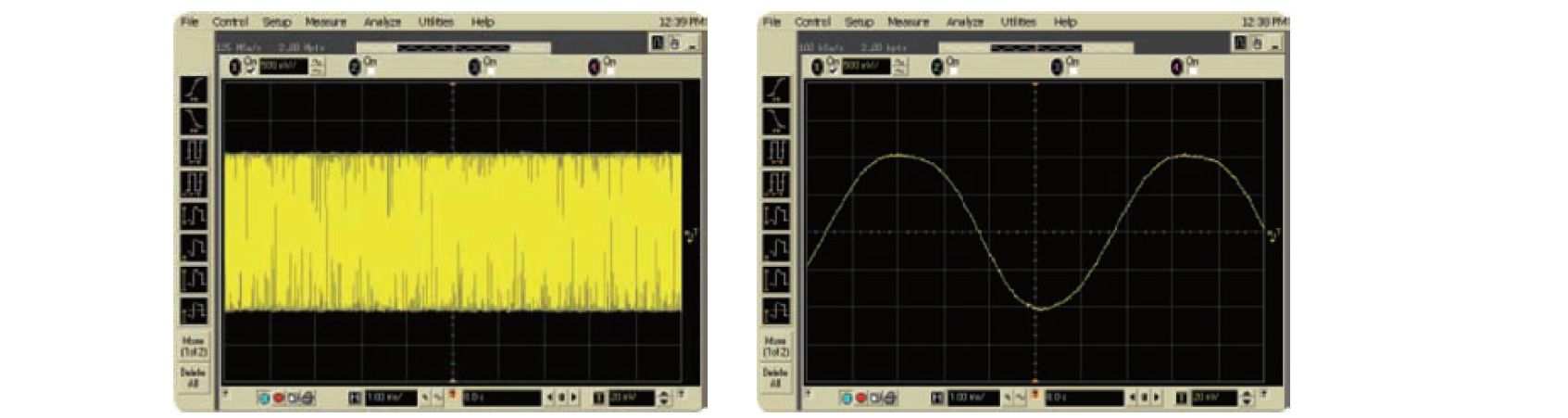
Figure 3: These images show an 80 MHz square wave acquired on an oscilloscope at a low sweep rate (1 ms/div) with the memory set to 2 Mpts on the left and 2 kpts on the right. The 2 Mpts deep memory maintains the highest sample rate to prevent signal aliasing. When the memory is reduced to 2 kpts, the sample rate is reduced by a factor of 1000. The reduced sample rate causes the oscilloscope to undersample the signal, resulting in an aliased signal at 155 MHz. Although the waveform on the right looks correct, it is not. The waveform frequency has shifted by 79.9 MHz.

5. What display features do you need on your oscilloscope?

All oscilloscope vendors know that they sell an image of a waveform. Back in the days of analog oscilloscopes, the design characteristics of the oscilloscope's CRT display determined the quality of the image. In today's digital world, an oscilloscope's display performance is determined more by the digital processing algorithms than by the physical characteristics of the display device.