Conversion between geocentric coordinates and rectangular coordinates in centric space
1 Glossary:
A: Geocentric space rectangular coordinate system:
a) The origin of the coordinate is the geocentric 0;
b) The Z axis coincides with the minor axis (rotation axis) of the reference ellipsoid;
c) The X axis coincides with the intersection of the starting meridian plane and the equator;
d) The Y axis is perpendicular to the X axis on the equatorial plane, forming a right-handed rectangular coordinate system 0-XYZ;
e) The position of the ground point P is represented by (X, Y, Z);
B: Geocentric geodetic coordinate system:
a) The origin of the coordinate is the center of the reference ellipsoid, and the minor axis of the ellipsoid coincides with the rotation axis of the reference ellipsoid;
b) Geodetic latitude B: The angle between the ellipsoid normal passing through the ground point and the equatorial plane
of the ellipsoid is the geodetic latitude B; c) Geodetic longitude L: The angle between the ellipsoid meridian plane passing through the ground point and the starting meridian plane is the geodetic longitude L;
d) Geodetic height H: The distance from the ground point to the ellipsoid surface along the ellipsoid normal is the geodetic height H;
e) The position of a ground point is represented by (B, L, H).
2 Convert the geocentric coordinates to the geocentric space rectangular coordinates:

In the formula, N is the radius of curvature of the ellipsoidal surface, e is the first eccentricity of the ellipsoid, a and b are the major and minor radii of the ellipsoid, f is the flattening of the ellipsoid, and W is the first auxiliary coefficient.
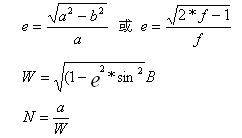
3. Conversion of centric spatial rectangular coordinates to centric geodetic coordinates
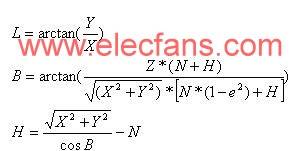
2. Gauss projection and Gauss rectangular coordinate system
1.
Overview of Gaussian Projection
Conditions of Gaussian-Krüger projection: 1. It is a conformal projection; 2. The central meridian is not deformed
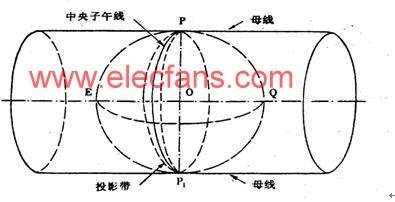
Gauss projection properties: 1. The angle remains unchanged after projection; 2. The length ratio is related to the point position, not the direction; 3. The farther away from the central meridian, the greater the deformation
In order to control the length deformation after projection, the zoning projection method is used. The 3-degree or 6-degree zoning is commonly used. The coordinates of the city or engineering control network can use any zone that is not based on the 3-degree central meridian.
2. Gaussian projection forward calculation formula:
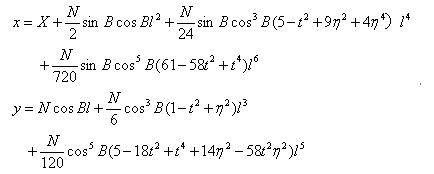
3. Gaussian projection inverse calculation formula:
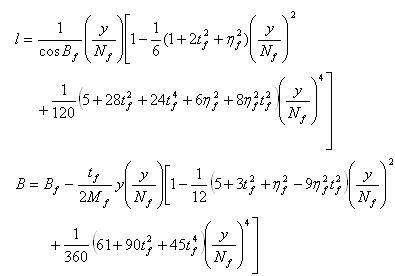
Previous article:Common volume calculation formulas
Next article:Introduction and working principle of servo motor
- Popular Resources
- Popular amplifiers
- High signal-to-noise ratio MEMS microphone drives artificial intelligence interaction
- Advantages of using a differential-to-single-ended RF amplifier in a transmit signal chain design
- ON Semiconductor CEO Appears at Munich Electronica Show and Launches Treo Platform
- ON Semiconductor Launches Industry-Leading Analog and Mixed-Signal Platform
- Analog Devices ADAQ7767-1 μModule DAQ Solution for Rapid Development of Precision Data Acquisition Systems Now Available at Mouser
- Domestic high-precision, high-speed ADC chips are on the rise
- Microcontrollers that combine Hi-Fi, intelligence and USB multi-channel features – ushering in a new era of digital audio
- Using capacitive PGA, Naxin Micro launches high-precision multi-channel 24/16-bit Δ-Σ ADC
- Fully Differential Amplifier Provides High Voltage, Low Noise Signals for Precision Data Acquisition Signal Chain
- Innolux's intelligent steer-by-wire solution makes cars smarter and safer
- 8051 MCU - Parity Check
- How to efficiently balance the sensitivity of tactile sensing interfaces
- What should I do if the servo motor shakes? What causes the servo motor to shake quickly?
- 【Brushless Motor】Analysis of three-phase BLDC motor and sharing of two popular development boards
- Midea Industrial Technology's subsidiaries Clou Electronics and Hekang New Energy jointly appeared at the Munich Battery Energy Storage Exhibition and Solar Energy Exhibition
- Guoxin Sichen | Application of ferroelectric memory PB85RS2MC in power battery management, with a capacity of 2M
- Analysis of common faults of frequency converter
- In a head-on competition with Qualcomm, what kind of cockpit products has Intel come up with?
- Dalian Rongke's all-vanadium liquid flow battery energy storage equipment industrialization project has entered the sprint stage before production
- Allegro MicroSystems Introduces Advanced Magnetic and Inductive Position Sensing Solutions at Electronica 2024
- Car key in the left hand, liveness detection radar in the right hand, UWB is imperative for cars!
- After a decade of rapid development, domestic CIS has entered the market
- Aegis Dagger Battery + Thor EM-i Super Hybrid, Geely New Energy has thrown out two "king bombs"
- A brief discussion on functional safety - fault, error, and failure
- In the smart car 2.0 cycle, these core industry chains are facing major opportunities!
- The United States and Japan are developing new batteries. CATL faces challenges? How should China's new energy battery industry respond?
- Murata launches high-precision 6-axis inertial sensor for automobiles
- Ford patents pre-charge alarm to help save costs and respond to emergencies
- New real-time microcontroller system from Texas Instruments enables smarter processing in automotive and industrial applications
- Input overvoltage and quiescent current of TPS62150
- Raspberry Pi PICO Macro Keyboard
- EEWORLD University Hall----Live Replay: Qorvo, muRata, Keysight Collaboration- New Opportunities in UWB Market
- List of problems in using CC1310
- [GD32L233C-START Review] V. I2C (Hardware I2C Driven OLED)
- How to prevent lithium battery from supplying power to load when charging
- [NXP Rapid IoT Review] + Rapid IOT Kit Review Summary
- Problems encountered when compiling code in CCS5
- Please give me some guidance on the route of analog electronics learning
- Worried about switching from Class AB to Class D? No need to worry

 LT1359CS14#PBF
LT1359CS14#PBF











 京公网安备 11010802033920号
京公网安备 11010802033920号