Approximate two-dimensional model of radar imaging and its super-resolution algorithm

Figure 1. 2D radar target geometry

Since the observation angle Δθ is very small, we take the approximation sin(nδθ)≈nδθ and cos(nδθ)≈1, then equation (2) can be approximately written as:

(3)

In the formula
The third term in the exponential term of formula (3) is the time-frequency coupling term, which is unique to the line frequency modulation signal (whose ambiguity function is an oblique ellipse). If a narrow pulse is used for transmission, this term does not exist. If this term is ignored, formula (3) becomes a commonly used echo two-dimensional sinusoidal signal model.
In fact, the third term of formula (3) is the "distance movement" term, which is proportional to the horizontal coordinate xk of the scattering point. It must be considered when the target area is large, and this is far from enough. The Doppler movement of the scattering point must also be considered. For this reason, let sin(nδθ)≈nδθ and cos(nδθ)≈1-(nδθ)2/2, then the more accurate approximation of formula (2) can be written as:

(4)

Compared with equation (3), equation (4) adds two terms to the index. The first term is the "Doppler shift" term. The larger the ordinate yk is, the greater the impact is. This can make up for the deficiency of equation (3). The second term is the Doppler shift term of time-frequency coupling. Since Mγ/Fs<

(5)

It should be pointed out that there is the following relationship between the parameters of each scattering point: ωk/μk=2γ/Fsfcδθ2 and k/vk=fcFs/γδθ. Since the radar parameters (fc,γ,Fs) and the motion parameters (δθ) are known, only three of the five parameters to be estimated are independent. This paper assumes that the five parameters are independent, and the relationship between the parameters has been considered in the imaging calculation.
Let {ξk}Kk=1≡{αk,ωk, k,μk,vk}Kk=1, now we want to estimate the parameter {ξk}Kk=1 from y(m,n).

3. Two-dimensional generalized RELAX algorithm
For the signal model shown in equation (5), let:

Y=［y(m,n)］M×N

Then in formula (6)

Assume that the estimated value of ξk is , then the estimation problem of ξk can be solved by optimizing the following cost function:

(7)

In the formula, ‖.‖F represents the Frobenius norm of the matrix, and ⊙ represents the Hadamard product of the matrix.
The optimization of C1 in the above formula is a multidimensional space optimization problem, which is very complicated. This paper generalizes the RELAX［3］ algorithm to solve it. To this end, we first do the following preparation work, let:

(8)

That is, assuming that { i}i=1,2,…,K,i≠k has been found, then the minimization of C1 in equation (7) is equivalent to the minimization of the following equation:

C2(ξk)=‖Yk-αk(aM(ωk)bTN( k)Pk)⊙Dk(vk)‖2F　(9)

Let: Zk=YkP-1k⊙Dk(-vk) (10)
Since Pk is a unitary matrix, the modulus of each element of the matrix Dk |Dk(m,n)|=1, and it is obvious that the F norm of the matrix Yk and Zk is the same, so the minimization of C2 is equivalent to the minimization of the following formula:

C3=‖Zk-αkaM(ωk)bTN( k)‖2F　(11)

By finding the minimum value of αk for the above formula, we can obtain the estimated value k of αk:

k=aHM(ωk)Zkb*N( k)/(MN) (12)

From equation (12), we can see that: is the value of the normalized two-dimensional discrete Fourier transform of Zk at {ωk, k}, so as long as the estimated value { k, k, k, k} is obtained, k can be obtained by 2D-FFT . After substituting the estimated value k into equation (11), the estimated value { k, k, k, k} can be optimized by the following equation:

(13)

It can be seen from the above formula that for a fixed value of {μk, vk}, the estimated value { k, k} is the two-dimensional frequency value at the main peak of the normalized periodogram |aHM(ωk)Zkb*N( k)|2/(MN). In this way, the optimization problem of formula (13) is reduced to: find a point { k, k} within the possible range of values ​​on the (μk, vk) plane , at which the main peak of the periodogram |aHM(ωk)Zkb*N( k)|2/(MN) is larger than the main peaks at the other points. Therefore, we obtain the estimated value { k, k } of {μk, vk} through the above two-dimensional optimization , and then obtain the estimated value {k, k} of {ωk, k} from formula (13) . k}. In practice, in order to speed up the calculation, the optimization of the two-dimensional (μk, vk) plane can be implemented using the function Fmin() in Matlab. After the above preparations, the parameter estimation steps based on the generalized RELAX algorithm are as follows: Step 1: Assume that the number of signals K = 1, and use equations (13) and (12) to calculate 1. Step 2 (2): Assume that the number of signals K = 2, first substitute the 1 obtained in the first step into equation (8) to obtain Y2, and then use equations (13) and (12) to calculate 2; substitute the calculated 2 into equation (8) to obtain Y1, and then use equations (13) and (12) to recalculate 1. This process is repeated until convergence. Step 3: Assume that the number of signals K = 3, first Substitute 1 and 2 obtained in the second step into formula (8) to obtain Y3, and then use formula (13) and formula (12) to calculate 3; substitute the calculated 3 and 2 into formula (8) to obtain Y1, and then use formula (13) and formula (12) to recalculate 1; substitute the calculated 1 and 3 into formula (8) to obtain Y2, and then use formula (13) and formula (12) to recalculate 2. This process is repeated until convergence. Remaining steps: Let K = K + 1, and continue the above steps until K is equal to the number of signals to be estimated. The convergence criterion in the above process is the same as that of the RELAX algorithm, that is, compare the change value of the cost function C1 in the two iterative processes. If this change value is less than a certain value, such as ε = 10-3, the process is considered to converge.

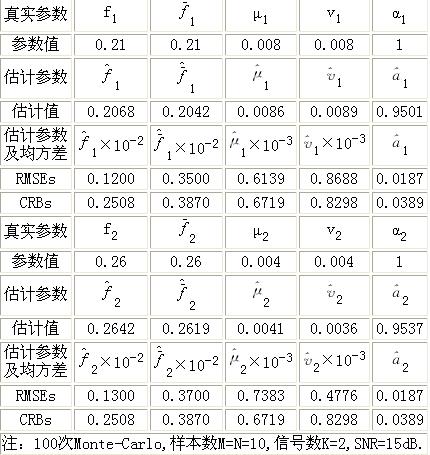
IV. Numerical simulation
1. Algorithm parameter estimation performance simulation
The simulation data is generated by equation (5), M=10, N=10, and the number of signals K=2. The signal parameters and experimental conditions are shown in Table 1, which is complex Gaussian white noise. Note that the frequency difference between the two signals is less than the FFT resolution Δf=Δω/(2π)=0.1. Table 1 gives the statistical results of the root mean square error of signal parameter estimation and the CR bounds for the corresponding situations. It can be seen that the estimated root mean square error is very close to the CR bound. In addition, the table also gives the estimated mean, which is also very close to the true value.

Table 1 Parameter estimation, CRB and comparison with RMS error for two-dimensional signals

Figure 2 RELAX imaging results under range movement error

Figure 3: Distance movement error

Fig.4 Signal intensity estimated by RELAX method and generalized RELAX imaging results

Figure 5 Signal strength estimated by generalized RELAX method

Appendix: CR bounds for parameter estimation
Below we give the CR bound expression for parameter estimation of two-dimensional signals as shown in equation (5). At the same time, it is assumed that the additive noise in equation (5) is zero-mean Gaussian colored noise, and its covariance matrix is ​​unknown. Let:

y=vec(Y) (A.1)
e=vec(E) (A.2)
dk=vec(Dk) (A.3)

Where vec(X)=(xT1,xT2,…,xTN)T, and vector xn(n=1,2,…,N) is the column vector of matrix X. We rewrite equation (5) into the following vector form:

(A.4)

In the formula , represents the Kronecker product, Ω=［{［P1bN( 1)］ aM(ω1)}⊙d1…{［PkbN( K)］ aM(ωK)}⊙dK］, α=(α1，α2，…，αK)T.
Let Q=E(eeH) be the covariance matrix of e, then for the two-dimensional signal model shown in formula (A.4), the Slepian-Bangs formula generalized for the ijth element of its Fisher information matrix (FIM) is［5,6］:
(FIM)ij=tr(Q-1Q′iQ-1Q′j)+2Re［(αHΩH)′iQ-1(Ωα)′j］ (A.5)
In the formula, X′i represents the derivative of the matrix X with respect to the i-th parameter, tr(X) is the trace of the matrix, and Re(X) is the real part of the matrix. Since Q is independent of the parameters in Ωα, and Ωα is also independent of the elements of Q, it is obvious that FIM is a diagonal matrix. Therefore, the CR bound matrix of the parameter to be estimated is obtained from the second term of (A.5).

令：η=(［Re(α)］T［Im(α)］TωT TμTvT)T (A.6)

In the formula, ω=(ω1，ω2，…，ωK)T, μ=(μ1,μ2,…,μK)T, =( 1， 2，…， K)T, v=(v1,v2,…,vK)T.
Let: F=［Ω jΩ DωΘ D Θ DμΘ DvΘ］ (A.7)
In the formula, the k-th column of the matrices Dω, D , Dμ, Dv are: ［{［PkbN( k)］ aM(ωk)}⊙dk］/ ωk, ［{［PkbN( k)］ aM(ωk)}⊙dk］/ k, ［{［PkbN( k)］ aM(ωk)}⊙dk］/ μk, ［{［PkbN( k)］ aM(ωk)}⊙dk］/ vk, Θ=diag{α1 α2 … αK}. Then the CRB matrix with respect to the parameter vector η is

CRB(η)=［2Re(FHQ-1F)］-1 (A.8)