Design of Parallel Multiply-Add Unit with Saturation Processing Function

Figure 1 Saturated MAC structure diagram

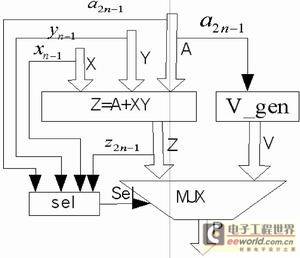
Figure 2 Optimized saturated MAC structure diagram

Introduction
In some digital signal processing applications, such as digital filtering, speech coding, and graphics processing, saturation operations are performed repeatedly. The so-called saturation operation means that when two n-bit operands are operated on, if the result overflows, the saturation value is taken. For an n-bit binary number represented by a two's complement code, the positive saturation value is 011...11, and the negative saturation value is 100...00. Saturation operations generally take two cycles, with arithmetic operations in the first cycle and saturation operations in the second cycle. More complex operations, such as MAC operations, generally perform saturation operations after completing multiplication and addition operations respectively, which usually requires more cycles. Parallel saturation operations obtain the results of serial operations within one cycle, which requires more hardware circuits to implement.
This paper designs a MAC unit to implement the operation of

=> with saturation processing function.

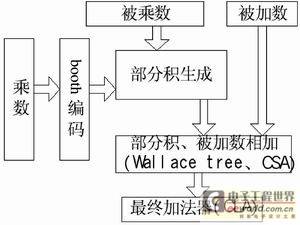
Figure 3 Block diagram of a 24×24 high-speed multiplier-adder

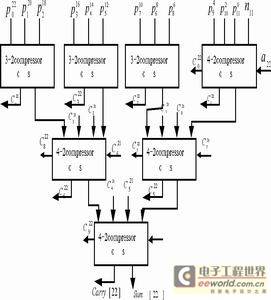
Figure 4 The largest Wallace tree structure in a parallel multiplier-accumulator

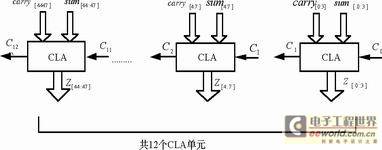
Figure 5 Implementation of the final adder

Basic structure of saturated multiplication and addition unit
In order to realize the saturation operation of

=>, in general, when calculating P, X and Y can be multiplied by the multiplier, and then the product is added to A. If overflow occurs, the sum is corrected to the saturation value. This is actually a simple series connection of the multiplier and the adder, and then the saturation value correction is performed, as shown in Figure 1. However, the MAC unit implemented with this structure has two levels of series adders on the critical path, because the final adder and the adder in the multiplier are simply connected in series, and the area and delay are relatively large.
In order to improve the performance of the MAC unit, this paper optimizes the structure mentioned above, and the optimized structure is shown in Figure 2. The addend of the MAC unit is used as a partial product of the multiplier and participates in the partial product addition array, so that the operation of adding after completing the multiplication calculation can be omitted, shortening the delay on the critical path.

High-speed parallel multiplication and addition unit structure
This paper uses the modified booth algorithm and Wallace tree structure to implement a 24×24 high-speed parallel multiplier. Figure 3 is a block diagram of the 24×24 high-speed multiplier and adder, which is mainly composed of booth coding, partial product array, Wallace tree and final adder.
Booth coding
The multiplicand and multiplier are signed numbers represented by n-bit complement codes. In MBA (modified booth algorithm):
the number of partial products =, without loss of generality, only the case where n is an even number is discussed here.
Let: X=-an-12n-1+2i;
Y=-bn-12n-1+2i;
According to MBA, the multiplier is transformed as follows:
Y=-bn-12n-1+2i
=
Here a-1=0;
Let i=0,1,2,…(n/2-1); Then
;
;
From the above formula, it can be seen that the amount of addition calculation is reduced by half, and it can be seen that Ki+1X needs to be shifted left by two bits relative to KiX.
In MBA, the multiplier is divided into 2-bit blocks. For the jth block, the 2 bits (b2j+1, b2j) in the block and the high bit b2j-1 in the previous block are re-encoded. The encoding truth table is:
Sign extension and partial product generation
In the partial product generation process, the extension of the sign bit is generated together with the partial product. We add all the extended sign bits:

Since the sum is 48 bits, the first term in the above formula is discarded, and we get:
;
For the generation of partial products, if the multiplier Ki is negative after booth recoding, the partial product needs to be inverted and then added to 1, as shown in Table 1. Therefore, in the design, the last bit of each partial product can be added to ni, and ni=1 when the booth encoding value is negative; ni=0 when the encoding value is positive.
Adding partial products and summands
Wallace tree is an implementation structure that improves the circuit speed by increasing the parallelism of the circuit. It adds all partial products to the circuit independently and in parallel at the same time, thereby improving the operation speed. In the Wallace tree structure, we use compression units to add the partial products and summands generated during the multiplication operation. In this design, we treat the summand as a partial product and add it to the Wallace tree array, so that the operation delay of performing the addition operation after completing the multiplication operation can be omitted, thereby improving the speed of the MAC unit.
The largest tree consists of three 3-2 compression units and four 4-2 compression units. The tree has only three levels of height, which is much smaller than the height when only full adders are used, and the delay is also much smaller. For other smaller trees, it can be achieved by reducing the number of compression units. Figure 4 shows the largest Wallace tree structure in this MAC unit (where a22 is the corresponding bit of the addend). Final
adder
In the Wallace tree array, each column of the Wallace tree generates a preliminary carry term and a preliminary addition result. Finally, a fast adder must be used to add all the carry terms and addition results. In order to obtain higher performance, a carry-lookahead adder (CLA) is generally used. It can generate all the carry terms at the same time, so it can achieve extremely high speed. In the worst case, the delay is proportional to n. However, as the number of bits increases, the carry terms become more and more complex, and the area consumed accordingly becomes larger and larger, and the speed cannot be guaranteed. Research shows that the optimal number of bits for CLA is 4 bits, which can achieve the best compromise between speed and area. In this design, the addend has 48 bits in total, so it is divided into 12 blocks, each with 4 bits. The blocks are connected in series through inter-block carry. The carry of each block only affects the bits in this block and does not affect the bits of higher blocks. Figure 5 shows the implementation of the final adder.

Saturation detection and generation of saturation value
In this design, the following formula is used to detect whether the result overflows:

Where (Xn-1) is the sign of XY. In case of overflow, the saturation correction value is output through a 48-bit 2-to-1 MUX. The corrected saturation value can be calculated by the following formula:
V=
(a2n-1 is the sign bit of the addend)

Conclusion
In the implementation of the entire MAC unit, the optimized design adds the addend as part of the partial product to the Wallace tree array, thereby reducing one level of cascaded carry-lookahead adders on the critical path; the special saturation detection logic is used, so that there is no need to wait for the generation of the sum, so that the saturation detection operation can be performed in parallel with the multiplication and addition operation, and the delay of the saturation detection logic is excluded from the critical path delay. Compared with the design implementation before optimization, the speed of the MAC unit has been greatly improved. The area and delay of the optimized design implementation are concentrated on the four parts of partial product generation, Wallace tree array, final adder and 2-to-1 MUX.
Table 2 is a comparison of the area and delay before and after optimization. It can be seen from the table that both in terms of speed and area, there are great improvements after optimization.