Kirchhoff's laws in phasor form

The previous sections discussed the time domain relationship between voltage and current in resistors, capacitors, and inductors, as well as the corresponding phasor expressions. For simple circuits, we know that the voltage and current in the circuit are sinusoidal quantities with the same frequency as the applied excitation source. This conclusion can be extended to complex sinusoidal AC circuits in linear steady state. For complex linear circuits, if all excitation sources are sinusoidal functions of the same frequency, then the current and voltage of each branch are sinusoidal functions with the same frequency as the excitation source, and can be expressed in phasor form. The phasor calculation method can be used in circuit calculations.

The time domain expression of Kirchhoff's node current law is

(3-7-1)

Because all currents are sinusoidal functions of the same frequency, the time domain summation expression can be converted into a phasor summation form according to the derivation in Section 3 of this chapter:

(3-7-2)

This formula shows that for any node, the sum of the current phasors flowing out of the node is equal to zero. This is Kirchhoff's node current law in phasor form.

Kirchhoff's voltage law states that the sum of the voltage drops in any closed circuit is zero, that is,

(3-7-3)

Kirchhoff's voltage law can be obtained in phasor form

(3-7-4)

By making a phasor diagram of the node current or loop voltage, a closed phasor polygon can be obtained. The above two laws and phasor relationships can be used in the calculation and analysis of sinusoidal AC circuits. Here are a few examples to illustrate this.

Example 3-7-1 In the circuit of Figure 3-7-1a, we know that , find the value of .

Solution: According to Kirchhoff's voltage law, we get:

The phasor diagram of voltage is shown in Figure 3-7-1b.

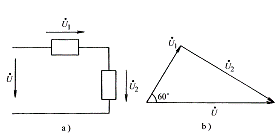
Figure 3-7-1