Basic principles and measurements of three-phase systems

Single-phase electricity is used to power domestic and office appliances, while three-phase alternating current (ac) systems are widely used to distribute power and directly supply power to higher-power devices. This article explains the basic principles of three-phase systems and the differences between the different possible measurement connections.

Three-phase system

Three-phase electricity consists of three AC voltages of the same frequency and similar amplitude. Each ac voltage "phase" is 120° apart from the other ac voltages (Figure 1). This can be represented graphically using waveforms and vector diagrams (Figure 2).

Figure 1. Three-phase voltage waveform

Figure 2. Three-phase voltage vectors

There are two reasons for using a three-phase system:

1. Three vector-spaced voltages can be used to generate a rotating magnetic field in the motor. This allows the motor to be started without the need for additional windings.

2. A three-phase system can be connected to the load, requiring half the number of copper cable connections (transmission losses) as other methods.

Let's look at three single-phase systems, each providing 100W of power to a load (Figure 3). The total load is 3 x 100W = 300W. To provide the power, 1 amp flows through 6 wires, so there are 6 units of loss. It is also possible to connect the three sources to a common return, as shown in Figure 4. The load is considered balanced when the load current in each phase is the same. When the load is balanced and the three current phases are shifted 120° from each other, the sum of the currents at any point in time is zero, and there is no current in the return line.

Figure 3. Three single-phase supplies – 6 unit losses

Figure 4. Three-phase power, balanced load – 3 unit losses

In a three-phase 120° system, three wires are required to transmit power, while in other systems six wires are required. The number of copper cables required is reduced by half, and the wire transmission losses are also reduced by half.

Y connection or star connection

A three-phase system with a common connection is usually shown in the schematic diagram of Figure 5, which is called a "Y-type or star" connection.

The common point is called the neutral point. For safety reasons, this point is usually grounded at the power source. In practice, loads are not perfectly balanced and a fourth "neutral" conductor is used to carry the resulting current. If local codes and standards allow, the neutral conductor may be much smaller than the three main conductors.

Figure 5. Y-connection or star connection – three-phase four-wire

Triangle connection

The three single-phase power supplies discussed above can also be connected in series. At any point in time, the sum of the three 120° phase-shifted voltages is zero. If the sum is zero, then both endpoints are at the same potential and can be connected together. This connection is shown in the schematic diagram in Figure 7 and is represented by the Greek letter Δ, which is called a delta connection. [page]

Figure 6. The sum of instantaneous voltages at any time is zero.

Figure 7. Delta connection – three phases and three wires

Comparison between Y-connection and triangle connection

The Wye connection is used to power everyday single-phase devices used in homes and offices. Single-phase loads are connected to one leg of the Wye between the line and neutral wires. The total load on each phase is shared as much as possible to provide a balanced load to the main three-phase power supply.

The wye connection can also provide single-phase or three-phase power to higher power loads at higher voltages. Single-phase voltage is the phase-to-neutral voltage. It also provides higher phase-to-phase voltages, as shown by the black vectors in Figure 8.

Figure 8. V phase-phase = √3 x V phase-neutral

The most common use of the delta connection is to supply power to higher power three-phase industrial loads. However, different voltage combinations can be obtained from the three-phase delta supply by making connections or "taps" along the transformer coils. For example, in the United States, a 240V delta system can have a split phase or center tap coil, providing two 120V supplies (Figure 9). For safety, the center tap point can be grounded at the transformer. Between the center tap point and the third "high leg" of the delta connection, 208V is also provided.

Figure 9. Delta connection with "split phase" or "center tap" coils

Power Measurement

In AC systems, power is measured using a wattmeter. Modern digital sampling wattmeters multiply multiple instantaneous samples of voltage and current together to calculate the instantaneous power, and then average the instantaneous power over a cycle to represent the active power. A wattmeter will accurately measure active power, apparent power, reactive load, power factor, harmonics, and more over a wide range of waveforms, frequencies, and power factors. In order for a power analyzer to provide good results, it is necessary to be able to correctly identify the wiring configuration and connect the power analyzer correctly.

Single-phase power meter connection

Only a wattmeter is required, as shown in Figure 10. The connection of the system to the voltage and current terminals of the wattmeter is simple and straightforward. The voltage terminal of the wattmeter is connected in parallel through the load, and the current is input through the current terminal in series with the load.

Figure 10. Single-phase two-wire and DC measurements

Single-phase three-phase connection

In this system, as shown in Figure 11, the voltages are generated from a center-tapped transformer coil, and all voltages are in phase. This is very common in North American residential applications, where one 240 V source and two 120 V sources are provided, and there may be different loads on each leg. To measure total power and other quantities, two wattmeters should be connected as shown in Figure 11.

Figure 11. Single-phase three-wire

Blondel's Theorem: Number of Power Meters Required

In a single-phase system, there are only two wires. The power is measured using one wattmeter. In a three-wire system, two wattmeters are required, as shown in Figure 12.

Generally speaking, the number of power meters required = number of lines - 1

Figure 12. Three-wire Y-type system[page]

Verifying a three-phase wye system

The instantaneous power measured by the power meter is the product of the instantaneous voltage and current samples.

Power meter 1 reading = i1 (v1 - v3)

Power meter 2 reading = i2 (v2 - v3)

The sum of the readings W1 + W2 = i1v1 - i1v3 + i2v2 - i2v3

= i1v1 + i2v2 - (i1 + i2)v3

(According to Kirchhoff's law, i1 + i2 + i3 = 0, so i1 + i2 = -i3)

2 readings W1 + W2 = i1v1 + i2v2 + i3v3 = total instantaneous power.

Three-phase three-wire connection – two power meter method

When there are three wires, two wattmeters are required to measure the total power. Connect the two phases to the voltage terminals of the wattmeter as shown.

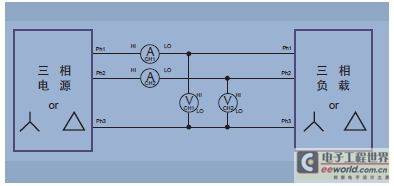
Figure 13. Three-phase, three-wire, two power meter method

Three-phase three-wire connection method – three power meter methods

As mentioned earlier, although only two wattmeters are required to measure the total power in a three-wire system, it is sometimes convenient to use three wattmeters. In the connection shown, a false neutral is created by connecting the low voltage terminals of all three wattmeters together.

Figure 14. Three-phase three-wire (three power meter method, set the analyzer to three-phase four-wire mode)

The advantage of the three-wire three-wattmeter connection is that it indicates the power in each phase (which is not possible in the two-wattmeter connection) as well as the phase-to-neutral voltage.

Three-phase four-wire connection

Measuring the total power in a four-wire system requires three wattmeters. The voltages measured are the true phase voltages. By using vector math, the phase-to-phase voltages can be accurately calculated from the magnitude and phase of the phase voltages. Modern power analyzers also use Kirchhall's law to calculate the current flowing in the neutral conductor.

Figure 15. Three-phase four-wire (three power meter method)

Configuring the measurement device

When the number of lines is certain (N), N-1 power meters are required to measure the overall power quality, such as power. You must ensure that there are a sufficient number of channels and that they are connected correctly.

Modern multi-channel power analyzers will directly calculate overall power quality such as watts, volts, amps, VA, and power factor using the appropriate built-in formulas. The formulas are selected based on the wiring configuration, so setting up the wiring is critical to getting a good overall power measurement. Power analyzers with vector capabilities will also convert the phase (or wye) voltage components to line (or delta) voltage components. Only a factor of √3 can be used to convert between systems or to calibrate measurements with only one wattmeter on a balanced linear system.

Understanding cabling configurations and making the correct connections is critical to power measurements. Being familiar with common cabling systems and remembering Blondel's theorem will help you make the right connections and get results you can rely on.