Traveling waves in uniform transmission lines

This section discusses the physical meaning of the sinusoidal steady-state solution of the long-line equation. From equation (10-3-6), we know that the voltage consists of two terms, the first term is (assuming ), write it as a time function, record it as , then:

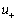
(10-4-1)

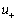is a function of time t and distance x , which can be written as . First fix a certain location, let , then:

(10-4-2)

In the formula, is the amplitude of the sine function, is the initial phase of the sine function. It can be seen that at a certain point is a sinusoidal oscillation of equal amplitude that changes with time. As shown in Figure 10-4-1.

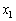
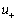
If we fix a certain time , then:

(10-4-3)

It is a decaying sinusoidal oscillation with amplitude varying with distance x .

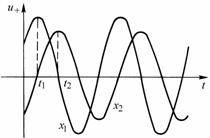
Figure 10-4-1

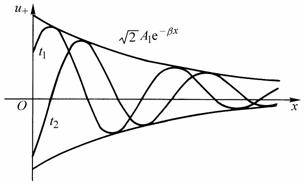
Figure 10-4-2

The two instantaneous distribution curves along the line are shown in Figure 10-4-2. They are decaying sine curves with as the envelope.

In summary, it is a traveling wave that advances in the direction of increasing x as time increases and gradually decays in the advancing direction. This traveling wave that advances from the power supply to the load is called a forward traveling wave.

The propulsion speed of the traveling wave is expressed by the moving speed of the point where the phase remains unchanged, which is called the phase speed and can be calculated by the following formula:

(10-4-4)

For overhead transmission lines, the phase velocity is the speed of light in a vacuum, ie .

The distance a traveling wave travels in one cycle is called its wavelength 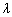, so:

(10-4-5)

The second term of voltage in formula (10-3-6) is (assuming ), and the corresponding time function is recorded as :

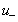
(10-4-6)

It is an attenuated wave that propagates along the direction of decreasing x with phase velocity , that is, an attenuated sine wave that propagates along the line from the terminal to the starting end, which is called a reverse traveling wave.

Similarly, the current I in formula (10-3-7) can also be decomposed into a direct current wave and a current echo wave, namely:

(10-4-7)

Now let's explain the meaning of characteristic impedance. From equations (10-4-6) and (10-4-7), we can see that:

(10-4-8)

Characteristic impedance is the ratio of incident voltage to incident current, also known as wave impedance.

Write the voltage and current as instantaneous function expressions:

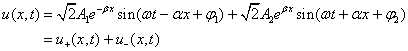(10-4-9)

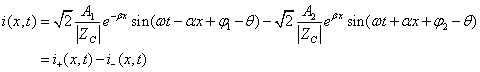(10-4-10)

In the formula: .

The ratio of the reflected voltage (or reflected current) to the incident voltage (or incident current) at any point along the transmission line is called the reflection coefficient N. It can be proved that:

(10-4-11)

Where: is the initial input impedance.

Another expression for N is:

(10-4-12)

On the terminal:

(10-4-13)

Where: is the terminal load impedance.