Permanent Magnet Synchronous Motor Control Based on Chaos Synchronization

In recent years, with the rapid development of high-power electronic devices, permanent magnet synchronous motors have been widely used in the fields of robotics and aerospace due to their high efficiency and good dynamic characteristics [1]. However, their application is greatly restricted due to the fact that their high-speed and weak magnetic field control are limited by high threshold voltage [2]. Studies have shown that permanent magnet synchronous motor systems, like many nonlinear systems, exhibit multiple steady-state operating points. Under certain conditions, limit cycles or even chaos may occur. Therefore, studying the characteristics of permanent magnet synchronous motor systems near steady-state operating points has become a hot topic in recent research. A large number of literatures show that permanent magnet synchronous motors have similar dynamic characteristics to chaotic Lorenz systems [3-5].
A chaotic system is a deterministic system whose motion trajectory is sensitively dependent on the initial state of the system. That is, two identical chaotic systems start from very close initial states, and after a certain transition time, their motion trajectories will become completely different. This is very similar to the characteristics exhibited by some complex systems in real life, that is, the randomness exhibited by deterministic systems. The chaotic characteristics of the system are undesirable in many cases, so many control methods have been studied to eliminate chaotic phenomena for these systems. For example, adaptive control of chaos[6], variable structure control[7], feedback control, etc.[8]. In addition, since the publication of Pecora and Carroll's article (i.e. PC synchronization method)[9], the research on chaos synchronization has also made great progress.
This paper is based on the viewpoint of chaos synchronization to design a state observer for permanent magnet synchronous motor, thereby constructing a nonlinear feedback controller to realize the control of permanent magnet synchronous motor. Through a simple linear system zero-pole configuration method, the desired operating characteristics can be obtained, and the chaotic phenomenon that may occur in PID correction due to improper parameters can be avoided.
1 Mathematical model
The dq model of permanent magnet synchronous motor is widely used in controller design. The AC variables of the motor can be easily converted into DC variables through Park transformation, which greatly facilitates the control system design. The dq model of permanent magnet synchronous motor can be expressed as:

2 Controller Design
Linear controllers, especially proportional-integral (PI) controllers, are usually the preferred design solution for permanent magnet synchronous motor speed control. It can be simply described as a double closed-loop control system: the inner loop is the current loop and the outer loop is the speed loop. Here, we take the proportional regulator as an example to illustrate the disadvantages of traditional linear regulators in permanent magnet synchronous motor control applications. Let Iqr and Idr be the command currents of the q-axis and d-axis respectively, and in practice Idr=0 can be easily guaranteed [4]. Then the dq voltage of the proportional regulator is:

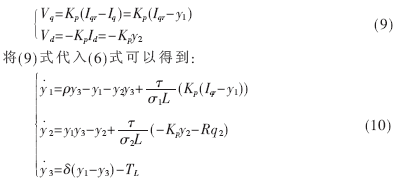
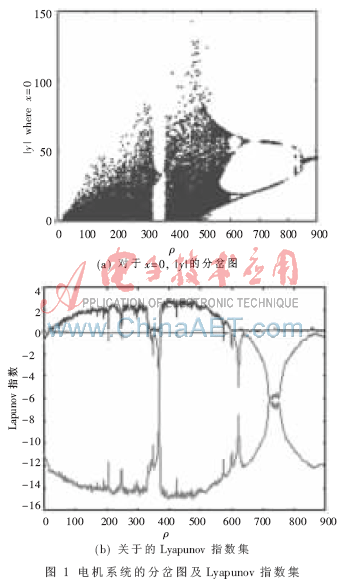
In order to obtain an undriven Lorenz system, the external torque TL can be set to 0, and the command current Iqr can be set to 0. The following model can be obtained:

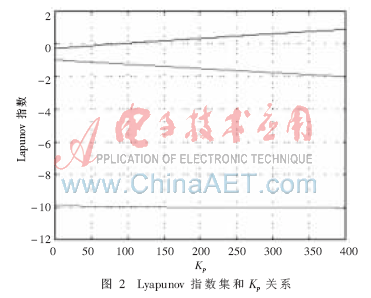
Substitute equation (7) into equation (11), and the relationship between the Lyapunov index set of the Lorenz system family and the feedback gain Kp can be obtained by calculation, as shown in Figure 2. The calculation method used in the figure is also the Wolf method, but this time the calculation of the Lyapunov index set is closely related to the feedback gain Kp.
It can be seen from Figure 2 that the permanent magnet synchronous motor can remain stable under a smaller feedback gain Kp (Kp<86), and the chaos gradually intensifies with the increase of Kp. When designing a control system, on the one hand, in order to ensure the response speed of the system, a larger feedback gain must be required; on the other hand, a large feedback gain can easily make the system chaotic. The same result is also obtained for the PI regulator. Inspired by nonlinear feedback [14], the following feedback can be introduced:

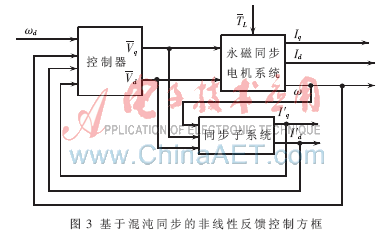
Through a simple zero-pole configuration method, the closed-loop system can obtain the desired performance. Furthermore, some variables in the actual system cannot be directly measured. For example, the synchronous motor position sensorless control currently studied can only measure the angular velocity of the motor. For this reason, a state observer based on chaos synchronization can be constructed to estimate other variables, so that control can be achieved. Its structural block diagram is shown in Figure 3. In other words, by constructing a synchronous subsystem related to the permanent magnet synchronous motor, the motor state variables required for control are replaced by the subsystem variables after synchronization, thereby forming a closed-loop control.

This paper first introduces the similarities between the permanent magnet synchronous motor and the chaotic Lorenz system in mathematical models. The permanent magnet synchronous motor itself does not exhibit chaotic characteristics, but with the change of the external torque of the motor and the change of the q-axis voltage, chaotic phenomena may occur. The traditional PI controller is not very effective in suppressing chaos. Therefore, nonlinear feedback control is introduced, which can transform the nonlinear motor system into an ordinary first-order system, so that the desired response characteristics can be achieved through the zero-pole configuration of the linear system. Considering that some variables of the actual system may not be measured, a state observer based on chaotic reduced-order synchronization is introduced on the basis of nonlinear feedback, and some unmeasurable variables are replaced by estimated values, thereby forming nonlinear feedback and realizing the control of the motor system. At the same time, the stability of the observer is proved by the Lyapunov direct method. The simulation results also prove the effectiveness of the controller.
References
[1] Wang Lixin, Wang Yune, Wang Fengxin. Control method of permanent magnet synchronous motor for electric vehicles based on DSP[J]. Journal of Electric Machines and Control, 2005,9(1): 51-54.
[2] JAHNS TM, KLINMAN GB, NEUMANN T W. Interior permanent magnet synchronous motors for adjustable-speed drives[J]. IEEE Transactions on Industrial Applications, 1986,22(4):738-747.
[3] HEMATI N, KWATNY H. Bifurcation of equilibria and chaos in permanent-magnet machines[C]. Proceedings of the 32nd conference on Decision and control, December 1993:425-429.
[4] Yang Zhihong, Yao Qionghui. Study on nonlinearity of brushless DC motor system[J]. Journal of Dynamics and Control, 2006,4(1):59-62.
[5] HEMATI N. Strange attractors in brushless DC motors. IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Application. 1994,41(1):40-45.
[6] LI Shuang, XU Wei, LI Rui Hong. Synchronization of two different chaotic systems with unknown parameters[J].Phys. Lett. A, 2007,361(1):98-102.
[7] LI Xiao Run, ZHAO Liao Ying, ZHAO Gu ang Zhou. Sliding mode control for synchronization of chaotic systems with structure or parameters mismatching[J]. Zhejiang Univ SCI, 2005(6):571-576.
[8] HUANG LL,WANG M, FENG R. Parameters identification and adaptive synchronization of chaotic systems with unknown parameters[J]. Phys. Lett. A, 2005,342:299-304.
[9] PECORA LM, CARROLL T M.Synchronization of chaos systems[J]. Phys Rev Lett, 1990,64(8):821-830.
[10] HEMATI N, LEU M C. A complete model characterization of brushless DC motors[J]. IEEE Transactions on Industry Applications. 1992,28(1):172-180.
[11] GE Zheng Ming, CHANG Ching Ming, CHEN Yen Sheng. Anti-control of chaos of single time scale brushless dc motors and chaos synchronization of different order systems[J]. Chaos, Solitons and Fractals, 2006,27:1298-1315.
[12] JING Zhu Jun, CHANG Yu, CHEN Guan Rong. Complex dynamics in a permanent-magnet synchronous motor model[J]. Chaos, Solitons and Fractals, 2004,22:831-848.
[13] GE ZM, CHENG J W. Chaos synchronization and parameter identification of three times scales brushless DC motor system[J]. Chaos, Solitons and Fractals, 2005, 24:597-616.
[14] ZAHER A A. A nonlinear controller design for permanent magnet motors using a synchronization-based technique inspired from the Lorenz system[J]. CHAOS, 2008,18:(1).