Nonlinear excitation control based on input-to-state feedback linearization

This paper applies the idea of ​​input-to-state feedback linearization to the generator excitation control system and obtains a set of practical generator nonlinear excitation control laws. The nonlinear control laws derived by the method of this paper are consistent with those derived by the state feedback precise linearization method, but the method proposed in this paper is simpler and more practical than the state feedback precise linearization method based on differential geometry theory. Simulations show that the nonlinear excitation controller proposed in this paper can suppress the oscillation of the system better than the conventional AVR+PSS when a large disturbance occurs in the system. It has a certain effect on enhancing the stability of the system.
Keywords: nonlinear; input-to-state feedback linearization; differential geometry; excitation control

Nonlinear excitation controller based on input-state linearization
HU Zhaoqing, MAO Chengxiong, LU Jiming

(Collage of Electrical Electronics Engineering, HuaZhong

University of Science and Technology, Wuhan 430074, China)

Abstract: The nonlinear excitation controller based on input-state linearization theory is proposed in this paper. The control law inferred from the proposed method has the coherence with the result deduced from the exact linearization based on theory of differential geometry; however, the method presented in this paper is more convenient and practical. Simulation results show that the proposed nonlinear controller can provide better damping characteristics than the general AVR+PSS when the power system is subject to the small or large disturbance.
Key words: nonlinear control; input-state linearization; differential geometry; excitation control

1 Introduction
The stability of power system operation is the basic requirement for safe operation of power system, and the control of synchronous generator excitation is an economical and effective means to improve the stability of power system operation. By applying appropriate control to the excitation of the generator, the stability of the power system under large and small disturbances can be improved [1-3]. In the past, the design of excitation controllers was usually based on the linearization method of the operating point, and the power system was treated as a linearized system. However, the nonlinearity of the power system determines the limitations of this method. The state feedback precise linearization method based on differential geometry theory was introduced into the design of generator excitation control system [6]. However, this method requires complex differential geometry mathematical tools. As an improvement, the literature [7-9] proposed a nonlinear excitation controller based on direct feedback linearization theory. This paper proposes a nonlinear excitation controller based on input-to-state feedback linearization. This method is practical, convenient and easy to understand. This paper conducts a detailed simulation study on this new excitation controller. The simulation results show that this nonlinear excitation controller has a certain effect on improving the stability of the power system under large and small disturbances.

2 Brief introduction to the theory of input-to-state feedback linearization
For a given single-input affine nonlinear system:

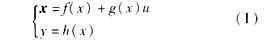
The condition that system (1) can be linearized by input-to-state feedback is that the system has a relative degree r=n, where n is the order of the system. If the nonlinear system (1) can be linearized by input-to-state feedback. Then 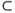there exists a differential homeomorphism T:Ω→Rn in a neighborhood Ω Rn. Under the new coordinate transformation z=T(x), the system can be transformed into:


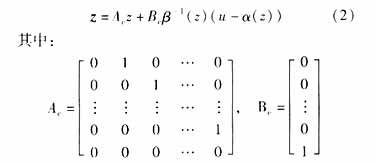
At the same time, the expressions of a(x) and B(x) can be obtained, as shown in equation (4).

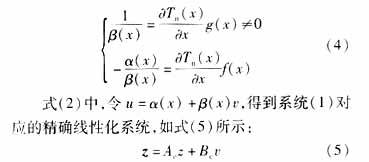
Equation (5) is a linearized system, so its control law can be designed completely according to the method of linear system.

3 Nonlinear excitation control design
The system to be studied is shown in Figure 1. The generator adopts a simplified third-order model. When the prime mover power is kept constant and the influence of friction damping is ignored, the system can be represented by the following set of differential equations:

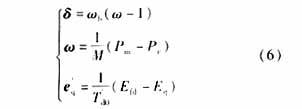
Where: δ is the generator power angle, Wb=2πf, W is the generator angular frequency, Pm is the prime mover power, Pe is the generator electromagnetic power, e′q is the transient potential, Efd is the excitation voltage, and Eq is the no-load potential. M is the inertia time constant, and T′do is the transient time constant of the excitation winding.

The system equation can be written as:

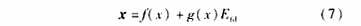
Since the system can realize the linearization of input to state feedback, there exists a reversible transformation z=T(x)=(T1(x) T2(x) T3(x))T to convert the system into the form of (5). From (3), we can get:

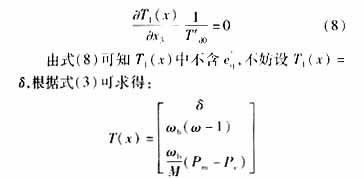
Its inverse transformation T-1(z) exists. According to equation (4), a(x), β(x) can be obtained.


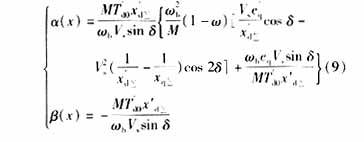
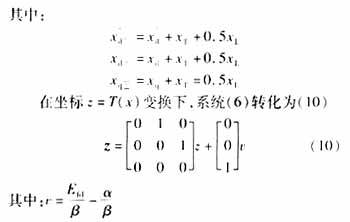
System (10) is a linear system. The control quantity can be designed according to linear optimal control [10]. The control quantity expression is shown in equation (11):

It can be proved that the control law derived by the input-to-state feedback linearization method is consistent with the control law derived by the state feedback exact linearization method based on differential geometry theory and the direct feedback linearization (DFL) method [6][8][9], but the method in this paper is simpler and more practical.

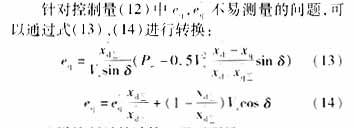
In this way, the calculation of the control quantity only requires the measurement of δ, W, and Pe.

4 Simulation results
For the system shown in Figure 1, the dynamic process of the system under two disturbances is simulated: (1) three-phase short circuit and fault removal after 0.2s; and (2) the double-circuit line operation is restored after the removal of one line for 3.5m. The simulation results are shown in Figures 2 and 3.

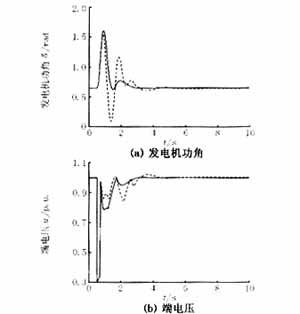
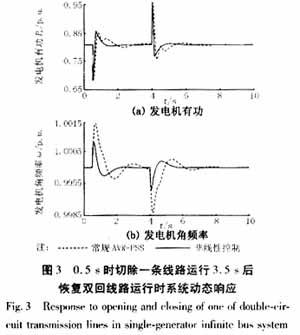
As can be seen from Figure 2 and Figure 3, the nonlinear excitation controller proposed in this paper always shows better damping characteristics than the conventional AVR+PSS when the system is disturbed. Therefore, the use of a nonlinear excitation controller can better suppress the oscillation of the system when a fault occurs, which has a certain promoting effect on enhancing the stability of the system.
In addition, this paper simulates the five-machine power system shown in Figure 4. Assuming that a three-phase short circuit occurs at the outlet of the No. 3 generator, a conventional AVR+PSS or a nonlinear excitation controller is installed on the No. 3 machine to examine the dynamic response of the multi-machine system. The simulation results are shown in Figure 5.

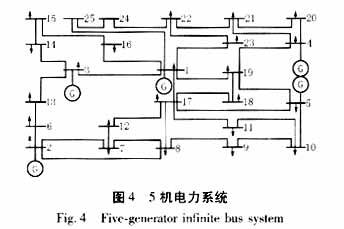
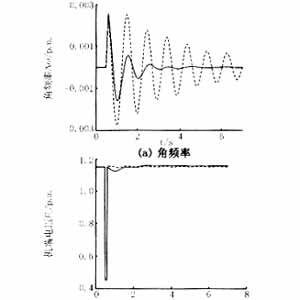
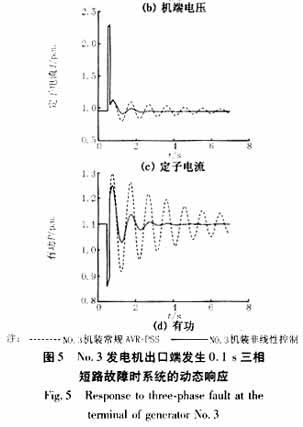
As can be seen from Figure 5, when the generator is equipped with the nonlinear excitation controller proposed in this paper, it can calm the oscillation faster than the conventional AVR+PSS when the system fails.

5 Conclusions
This paper proposes a nonlinear excitation controller based on the input-to-state feedback linearization theory. The obtained control law is consistent with the control law derived by the precise linearization idea based on differential geometry theory, but the method in this paper is simpler and more practical, which is conducive to engineering application. The simulation results of single-machine infinite system and multi-machine system prove that compared with the conventional AVR+PSS, the nonlinear excitation controller can better suppress the oscillation of the power system under large and small disturbances, and has a certain effect on enhancing the stability of the system.