Voltage-current relationship and difference of linear capacitors

When the reference direction of the voltage u across the capacitor is given, if q represents the charge on the reference positive potential plate, then the relationship between the charge and voltage of the capacitor satisfies

q = Cu

C represents the capacitance of the capacitor element. When the capacitor element is a linear element, C does not change with u and q, and is called a linear capacitor. It can be seen that the definition of a linear capacitor element is

C = q/u

When the unit of q is C and the unit of u is V, the unit of capacitance C is farad (F) from the above formula. The capacitance of an actual capacitor is often much smaller than 1F, so microfarad (μF) and picofarad (Pf) are often used in actual use.

From the above discussion, we can know that the qu plane, which is composed of u as the horizontal coordinate and q as the vertical coordinate, can be used to define a two-terminal capacitor element. The characteristic curve of a linear capacitor element on the qu plane is a straight line passing through the origin.

Voltage-current relationship of linear capacitor elements

Assume that voltage and current are time functions. Now find the relationship between voltage and current. When the voltage between the plates changes, the charge on the plates also changes, so a current is generated in the capacitor. This current can be obtained by the following formula

I = dq/dt = C (du/dt)

The above formula shows that the magnitude and direction of the current depends on the rate of change of voltage over time. When the voltage increases, du/dt>0, then dq/dt>0, i>0, the charge on the plate increases, and the capacitor is charged; when the voltage decreases, du/dt<0, then dq/dt<0, i<0, the charge on the plate decreases, and the capacitor discharges in the reverse direction. When the voltage does not change with time, du/dt=0, then I=0, and the current of the capacitor element is equal to zero, which is equivalent to an open circuit. Therefore, the capacitor element has the function of blocking direct current.

Energy storage characteristics of linear capacitor elements

The capacitor element does not generate energy or consume energy and is an energy storage element.

The difference between linear capacitors and nonlinear capacitors

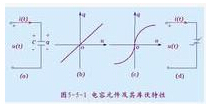
If the coulometric characteristic of a capacitor element is a straight line passing through the origin of the coordinate system, as shown in Figure 5-5-1(b), it is called a linear capacitor element. The capacitance C of a linear capacitor element is a constant and has nothing to do with the voltage u and current i. Its circuit symbol is shown in Figure 5-5-1(a). If the coulometric characteristic of a capacitor element is a curve of a certain shape passing through the origin of the coordinate system, as shown in Figure 5-5-1(c), it is called a nonlinear capacitor element. The capacitance C of a nonlinear capacitor element is not a constant and is related to the voltage u and current i. Its circuit symbol is shown in Figure 5-5-1(d).