Advantages of using an SMC-based arbitrary waveform generator to generate I/Q signals

In the rapidly developing cellular communication market, digital systems have replaced analog systems about ten years ago and have evolved from frequency division multiplexing (FDMA) and time division multiplexing (TDMA) systems to GSM and CDMA systems. Digital communication systems have been widely used in life. They have obvious advantages in energy consumption, spectrum efficiency, quality and cost, so that the entire analog TV infrastructure must be replaced with digital communication. Because a large number of digital communication system architectures use I/Q signals (i.e., in-phase signals and orthogonal signals) in a rectangular coordinate system to describe data symbols, engineers must be able to generate accurate baseband I/Q signals for research, design and production testing.

In research, a flexible I/Q generation system is key to quickly prototype and evaluate the performance of new modulation methods and transceivers. In new product designs, I/Q signals will test a large number of I/Q modulator/demodulator physical layer parameters, such as phase and amplitude balance, DC bias, and input compression point. These parameters are also tested in production to ensure that gain error and phase error are minimized. These two parameters, gain and phase, are critical to reducing the error vector amplitude and correctly transmitting data.

Arbitrary waveform generators, such as the NI 5421, based on NI's Synchronization and Memory Core (SMC) architecture, offer several benefits for generating baseband I/Q signals used in the design and test of digital communications systems. The NI 5421 generator has the following features:
Multimodule synchronization to independently control the phase, amplitude, and offset of I-, I+, Q-, and Q+ signals
2x, 4x, or 8x data interpolation for an effective sampling rate of up to 400 MS/s
Fast download of test waveforms using the PCI bus for increased test throughput
Large onboard waveform memory for playing back long signal runs

The most flexible synchronization function

In addition to requiring minimal distortion and low jitter, general I/Q applications also require precise control of the signal's amplitude, phase, and DC offset. The values ​​of these three parameters, amplitude, phase, and offset, are often changed in modulator testing. The input circuit of the modulator/demodulator is generally a differential circuit, including I-, I+ and Q-, Q+ signals. Although a differential signal can be generated by an AWG (arbitrary signal generator) and a transformer, four independent differential signals must be generated here to fully test the circuit design and clearly control the three parameters of phase, amplitude, and offset in three groups of differential signal pairs (I- and I+, Q- and Q+, and I/Q signal pairs). Traditional I/Q generators cannot adjust parameters in one differential pair, and this flexibility can only be achieved by synchronizing multiple independent AWGs. However, if multiple different AWGs are synchronized to generate differential signals, the skew and jitter between channels will distort the differential signals, so they must be attenuated.

Proper synchronization requires precise sample clock skew control, trigger delivery and skew control, and a low-jitter reference clock. This type of synchronization is often difficult or impossible to achieve in traditional GPIB-based AWGs and must be aided by some external cables and reference clocks, and even then, the results may still be problematic. The built-in trigger lines and 10MHz reference oscillator in the PXI platform make reliable synchronization between instruments easier to achieve. In addition, NI's T-Clock synchronization method (patent pending) provides a method to adjust the sample clock skew in steps of about 20ps to eliminate the effects of trigger skew.

T-Clock multi-module synchronization

Because NI 5421 devices are built on the SMC architecture, they provide precise T-Clock synchronization (see NI Synchronization and Memory Core: A Modern Mixed-Signal Test Architecture). In T-Clock, a clock trigger signal is sent and received at a much lower rate than the AWG sample clock. To generate this clock signal (called T-Clk), the sample clock on each device is individually stepped down to less than 10 MHz. A time-to-digital converter (TDC) is used to measure the offset of T-Clk relative to the 10 MHz PXI reference clock, automatically aligning the T-Clk signal on each device. To send a start trigger, the master AWG sends a trigger line pulse synchronized to the falling edge of T-Clk. All receiving AWGs (including the master AWG itself) receive the trigger pulse and begin generating signals on the next rising edge of T-Clk. Because the period of T-Clk is equal to or greater than 100 ns, there is enough time for the trigger pulse to be transmitted to all devices before the next rising edge arrives, ensuring that all generators start at the same time.

This approach results in channel-to-channel skew of ≤500 ps. To achieve even lower skew, the output of the AWG can be connected to a multichannel, high-bandwidth oscilloscope, which will provide more accurate phase measurements than the onboard TDC. The simplest way to measure phase is to configure the AWG to generate a sine or square wave and then check the phase difference at the voltage zero crossing. Next, the measurement is entered into NI's T-Clock software and overlaid with the TDC measurement. Using the external oscilloscope's measurement, the skew can be reduced to 10 to 20 ps. Figure 1 shows the output of two synchronized PXI-5421 modules, generating a 10-MHz sine wave after the sample clock delay has been manually adjusted. The graph shows that the skew is almost always between 10 ps and 20 ps. At 10 MHz, a 10-ps skew is equivalent to 0.036 degrees of phase—less than the 0.1 degree required for most I/Q applications. Using the sample clock delay adjustment value, the skew changes by only ±1 sample clock period at most if the adjustment step size is less than 20 ps. If a larger phase adjustment is needed, the sample can be moved from the start to the end of a waveform for positive phases, and from the end to the start of a waveform for negative phases. This control method is coarse, but the sampling clock delay adjustment provides finer control.

Figure 1. Two PXI-5421 modules generate a 10 MHz frequency with less than 20 ps skew between channels.

The high-resolution clocking mode provided by the Analog Devices AD9852 DDS (direct digital synthesis) chip in the PXI-5421 can significantly improve the sub-20 ps resolution of the sampling clock delay adjustment. The AD9852 has a 14-bit programmable phase offset register that can adjust the sampling clock phase in steps of (sampling clock period/16384) seconds. For example, if the sampling clock frequency is 100 MS/s, the phase can be adjusted in steps of 610 fs (femtoseconds). However, when using high-resolution clocking (assuming that the jitter of the PXI-5421 system is about 4 ps), this precise phase control can only be observed by a histogram of the measured phase over a large number of output waveform cycles. This is because the inherent clock jitter in the DDS clock generation is larger, which limits the use of high-resolution clocking. This jitter results in increased phase noise in the I/Q signals. At ±10kHz of the carrier frequency, the phase noise of the divided clock mode is -137 dBc/Hz; therefore, in order to achieve the best performance phase noise, it is advisable to use this divided clock mode.

The high-resolution clock not only provides precise phase offset control, but also provides a sampling clock frequency adjustment resolution of 1.06 µHz, which is a prerequisite for obtaining the appropriate chip rate for digital communication systems. For example, the chip/symbol rates of WCDMA and CDMA2000 are 3.84MHz and 1.2288MHz, respectively. Typically, each symbol of these signals uses 4 sampling values, so the sampling rates are 15.36MHz and 4.9125MHz, respectively. The high-frequency resolution of the PXI-5421 can generate the appropriate sampling rate for the waveform, and in the receiver stress test, accurately change the playback frequency to test the frequency sensitivity of the receiver.

Because the differential signal is generated by two independent AWGs, the jitter between channels is the main cause of distortion, so the jitter should be as low as possible. To measure this jitter, two AWGs generating 10MHz square wave signals are connected to a Tektronix CSA8000 communication signal analyzer. One of the square wave signals triggers the signal analyzer externally, and the other is connected to the CH 0 channel. Figure 2 shows the jitter histogram at the zero crossing. The RMS value of the jitter is 2.954ps, and 95.7% of the data is within ±2σ of the mean. In addition, the histogram is Gaussian, which means that the jitter may come from random noise processes in electronic components.

Figure 2. The PXI-5421's channel-to-channel jitter is 2.954ps.

In addition to the excellent synchronization performance of T-Clock, the NI T-Clock application program interface (API) also provides some convenient functions that can be used to synchronize four AWGs. The first virtual instrument phase locks all devices to the PXI 10 MHz reference clock and configures the start trigger. The second virtual instrument performs T-Clock alignment to synchronize the T-Clk signals of all AWGs. Then, the signal generation begins and the program is terminated until the signal generation ends. A simple example is shown in Figure 3.

Figure 3. Four virtual instruments perform the necessary work to accurately synchronize the AWGs.

Generating Differential Signals Using RF Transformers

Some production test systems do not require independent signal phase, amplitude, and DC bias control for the differential I/Q signal pairs. For these applications, two single-channel AWGs plus some external signal shaping circuits are sufficient to accomplish the task. In this configuration, the phase, amplitude, and DC bias can be controlled between the I and Q signals, not just between the I-, I+ and Q-, Q+ differential pairs.

The external shaping circuit required is very simple. An RF transformer is used to convert the output of the single-ended AWG into a balanced differential signal. If a center-tapped transformer is used, a low-cost analog output module can also be used to add a DC bias to the balanced signal.

When selecting an RF transformer, an important specification is insertion loss, which is the ratio of power lost from the input to the output of the transformer. Insertion loss varies with input frequency, so the signal will be distorted within the expected bandwidth. Therefore, it is important to choose a transformer that has low insertion loss over the signal bandwidth.

In addition, choose a transformer with a center-tapped secondary winding. Connecting the center tap to an analog output module (such as the NI PXI-6704 16-bit analog output module) adds a DC bias to the balanced signal. Because most I/Q applications require a ±1.5 V DC bias, a resistive voltage divider circuit is used at the output of the PXI-6704 to reduce its ±10 V output voltage, thereby ensuring that full 16-bit amplitude control can be achieved within a smaller voltage range.

Because the two windings before and after the center tap are rarely the same, a bypass capacitor is added to the circuit to connect the center tap to the AC ground to maintain the balance of the transformer. The complete circuit is shown in Figure 4.

Figure 4. A single AWG can generate a differential signal using a center-tapped RF transformer, voltage divider, and capacitors.

Insertion loss and impedance mismatch cause the signal amplitude at the transformer output to be smaller than the expected amplitude at the AWG output. If the insertion loss is constant over the expected frequency range, it can be modeled with a resistor. Adding this resistor to the input impedance of the transformer calculates the effective impedance at the transformer output. The NI-FGEN driver function uses this value to adjust the output voltage of the NI 5421 to compensate for the impedance mismatch between the transformer and the 50 Ω output impedance of the NI 5421.

Data interpolation to improve spectral purity

I/Q signal generation applications place high demands on the spectral purity of the signal generator. To minimize the image distortion during the reconstruction of the digital-to-analog converted signal, the NI 5421 generator uses a combination of digital filters and analog filters to optimize passband flatness, phase linearity, and image rejection.

The sampling frequency of the DAC must be at least twice the bandwidth of the analog signal you want to generate. Although the theoretical minimum sampling frequency fs is twice the signal bandwidth fo, image components will appear on |fo ± nfs| in the output signal, as shown in Figure 5. These image components will reduce the spectral purity of the signal and must therefore be removed using a low-pass filter.

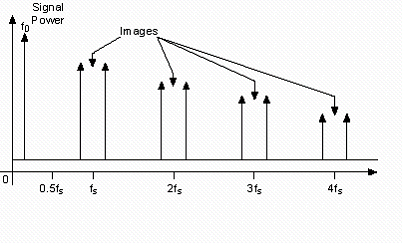
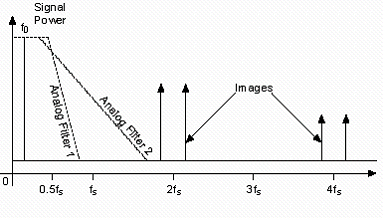
To understand signal interpolation and its effect on spectral purity, let’s assume there are three different analog filters with different cutoff frequencies and orders. These three filters and their sampled images are shown in Figure 6. “Analog Filter 1” is the ideal analog filter. Because this filter has very steep attenuation, it is the most expensive to implement and requires a lot of board space. It also does not achieve the passband flatness required for I/Q applications. Analog Filter 2 is a more practical filter, but it does not attenuate the image components near fs. In analog filters, there is a trade-off between attenuation after the cutoff frequency and flatness before the cutoff frequency; therefore, setting the ideal filter parameters depends largely on the sampling rate of the DAC and the frequency of the waveform being generated. It is almost impossible to achieve variable sampling and output signal frequencies with only one analog filter and meet stringent performance requirements.

Another key indicator of analog filters is group delay, which is the time required for a signal of finite length (such as a pulse signal) to pass through the analog filter. In an ideal filter with linear group delay, all frequency components in the signal have the same delay, so the phase of the output signal will not be distorted.

The third filter, analog filter 3, has a much higher cutoff frequency than the previous two filters. Because the cutoff frequency is so high, the filter passband (0 to 0.43fs) is very flat. The image components at fs and 2fs fall within the passband of filter 3, so there is no attenuation at all, but this phenomenon can be mitigated by using a digital interpolation filter.

To simplify the analog filter requirements and get good results over a range of sampling rates and output frequencies, the NI 5421 device uses a half-band finite impulse response digital filter to interpolate 1, 3, or 7 values ​​between every two samples of the waveform at 2, 4, or 8 times the sampling frequency (fs). Therefore, the effective sampling rate is equal to 2 times (2fs), 4 times (4fs), or 8 times (8fs) the original sampling frequency. The DAC then runs internally at this effective sampling rate—specifically, data is read from memory to the DAC at this rate.

In Figure 7, a 2x interpolation filter is used to increase the effective sampling rate of the DAC to 2fs. The first set of reconstructed images are located at |2fs ± fo|, which falls into the stopband range of filter 2.

In this way, the analog filter 2 can conveniently filter out all image components generated in the digital signal, as shown in the frequency domain in FIG. 7 and the time domain in FIG. 8 .

Using 2x interpolation filtering to increase the effective sampling rate of the DAC to 2fs can better remove image components and generate a signal with better spectral purity. However, if the interpolation filter is increased to 4x, the output signal can be further improved.

Figure 9 shows the image signal after using 4x interpolation and a DAC with an effective sampling frequency of 4fs. The image component is moved to 4fs, which is greater than the cutoff frequency of filter 3. This configuration used in the NI 5421 can remove spectral images and has the flattest passband characteristics. This configuration is close to the ideal method of digitally generating spectrally pure waveforms. The NI 5421 has a passband flatness of ±0.25 dB (40MHz) and a total harmonic distortion of -75dB at 1MHz.

Using PCI/PXI to reduce waveform download time

Test waveforms for digital communication systems can be very large. For example, when generating a WCDMA signal with a pseudo-noise sequence (PN sequence, 65,635 symbols) of order 16, the generated signal size is 3.15MB. To improve the statistical confidence of the measurement, larger PN sequences should be used. Using GPIB (IEEE 488 bus) to download waveforms larger than a few hundred kB can be very slow and seriously affect the test throughput. Although High Speed ​​GPIB (HS488) is an IEEE standard, few instruments can implement the 8 MB/s speed transfer mode. Although the GPIB standard specifies a theoretical throughput of 1 MB/s, GPIB-based instruments generally only achieve a throughput of 200-300 kB/s.

With a highly optimized driver and SMC architecture, the NI 5421 can achieve download rates of up to 84 MB/s for large data downloads. This rate can be attributed to the high throughput of the PCI bus; however, similar to GPIB, few external plug-in boards can actually reach the theoretical maximum PCI throughput of 132 MB/s.

Waveform size (I16 samples)	NI 5421 Averaging Time (s)	Average time of GPIB AWG (s)	Average speed of PCI/PXI
10,000	0.000610	0.151	247x
50,000	0.001924	0.807	419x
100,000	0.003442	1.724	501x
500,000	0.012714	8.149	641x
1,000,000	0.025005	16.460	658x

Table 1. The high-throughput PXI platform is 247 to 650 times faster than GPIB when downloading data to an AWG.

Large memory for generating long-duration signals

The SMC architecture can provide up to 256MB of memory for a single-channel NI 5421 arbitrary waveform generator. Because each sample value is 16 bits, the memory size should be 128MS (calculated based on the number of samples). If the sample rate is 100 MS/s, the playback time is 1.28s. If the digital interpolation method of the NI 5421 is used and the interpolation mode is selected as 8 times, the playback time can be extended to 2.56s. The 50 MS/s digital signal input to the DAC will be interpolated to 400 MS/s before being converted to an analog signal. If you want to generate grid and nebula plots and calculate bit error rates, a large data set will increase the statistical confidence of the measurement results. Large memory can generate non-periodic signals as long as possible, greatly improving the authenticity of the measurement. If you use an AWG with small memory and use a looping method to generate long signals, the periodic signal components will affect the test results and the device will not be fully tested. Because pseudo-random sequences are an important tool for describing the performance of communication systems, the long non-periodic signals generated by AWGs with large memory are very important for statistical measurements.

Creating I and Q Data

There are a number of tools available for generating I and Q waveform sample data. The data is simulated using a math toolkit such as MATRIXx X-Math or MathWorks MATLAB® software and is typically stored to disk. NI LabVIEW and LabWindows/CVI can read large amounts of data and convert them to 16-bit integers or double-precision floating-point numbers—two formats that the NI-FGEN driver can directly accept. The AWG first normalizes the waveform data to a ±1 V range and extracts the gain factor, then fully utilizes all 16 bits of the DAC and uses front-end analog electronics to amplify or attenuate the output signal to ensure optimal output signal quality.

LabVIEW can also generate I/Q data directly using the NI Modulation Toolkit. The Modulation Toolkit uses LabVIEW virtual instruments to perform modulation and demodulation of analog and digital signals (such as AM, FM, PM, QPSK, and QAM). Figure 10 shows how to use the toolkit to generate I and Q data for an FM signal. Using the first virtual instrument, select a standard waveform (such as sine, square, or triangle) and specify the carrier frequency and frequency offset to generate the FM message signal. The second virtual instrument performs the modulation and returns the complex envelope of the FM signal. Finally, both virtual instruments extract the I and Q data from the complex envelope signal and download it to the AWG. The toolkit can also modulate a custom message signal and extract the amplitude and phase components of the modulated signal (in polar coordinates) to test polar-based digital modulators. Waveform generation routines for other modulation methods (such as QAM and QPSK) can also be implemented using a similar structure.

Figure 10. Generate I and Q waveform data for an FM signal using the Modulation Toolkit for NI LabVIEW.

To simulate channel effects, the Modulation Toolkit provides Rayleigh and Rician fading models, or you can create a custom fading model based on the output of the simulation tool. To rigorously test the demodulator designed by the Modulation Toolkit, you can add interference such as quadrature skew and additive white Gaussian noise (AWGN) to the IQ signal to more accurately simulate the actual operating environment.