Oscilloscope sampling rate and memory depth

Bandwidth, sampling rate and memory depth are the three key indicators of digital oscilloscopes. Compared with engineers' familiarity and attention to oscilloscope bandwidth, sampling rate and memory depth are often overlooked in oscilloscope selection, evaluation and testing. The purpose of this article is to help engineers better understand the important characteristics of these two indicators and their impact on actual testing by briefly introducing the relevant theories of sampling rate and memory depth combined with common applications. At the same time, it helps us master the trade-off method of selecting oscilloscopes and establish the correct concept of using oscilloscopes.

Before we begin to understand the concepts related to sampling and storage, let us first review the working principle of the digital storage oscilloscope.

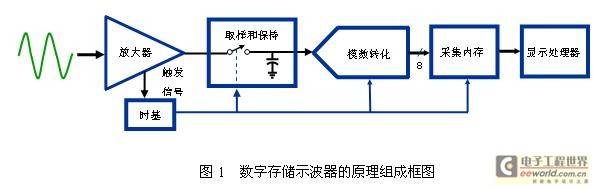
The input voltage signal is sent to the front-end amplifier after the coupling circuit, and the front-end amplifier amplifies the signal to improve the sensitivity and dynamic range of the oscilloscope. The signal output by the amplifier is sampled by the sampling/holding circuit and digitized by the A/D converter. After A/D conversion, the signal is converted into digital form and stored in the memory. The microprocessor processes the digitized signal waveform in the memory accordingly and displays it on the display. This is the working process of the digital storage oscilloscope.

Sampling, sampling rate
We know that computers can only process discrete digital signals. The first problem faced after the analog voltage signal enters the oscilloscope is the digitization (analog/digital conversion) of the continuous signal. The process from continuous signal to discrete signal is generally called sampling. Continuous signals must be sampled and quantized before they can be processed by computers. Therefore, sampling is the basis for digital oscilloscopes to perform waveform operations and analysis. The sampling of digital storage oscilloscopes is to measure the voltage amplitude of waveforms with equal time intervals and convert the voltage into digital information represented by eight-bit binary code. The smaller the time interval between the sampled voltages, the closer the reconstructed waveform is to the original signal. The sampling rate is the sampling time interval. For example, if the sampling rate of the oscilloscope is 10G times per second (10GSa/s), it means that a sample is taken every 100ps.

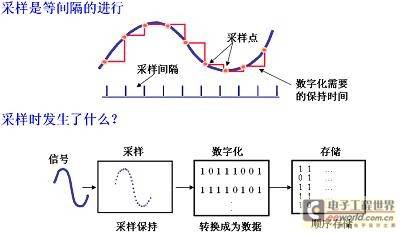
Figure 2 Oscilloscope sampling

According to the Nyquist sampling theorem, when sampling a band-limited signal with a maximum frequency of f, the sampling frequency SF must be greater than twice f to ensure that the original signal can be completely reconstructed from the sampled values. Here, f is called the Nyquist frequency, and 2 f is the Nyquist sampling rate. For a sine wave, at least two samples are required per cycle to ensure that the digitized pulse sequence can accurately restore the original waveform. If the sampling rate is lower than the Nyquist sampling rate, aliasing will occur.

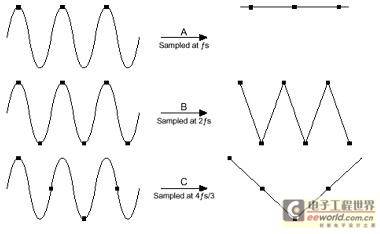
Figure 3 Sampling rate SF < 2 f, aliasing distortion [page]

The waveforms shown in Figure 4 and Figure 5 look very similar, but the frequency measurement results are very different. Which one is correct? A careful observation will reveal that the trigger position and trigger level in Figure 4 do not correspond, and the sampling rate is only 250MS/s, while Figure 5 uses a sampling rate of 20GS/s. It can be determined that the waveform shown in Figure 4 deceives us. This is an example of aliasing caused by a low sampling rate.

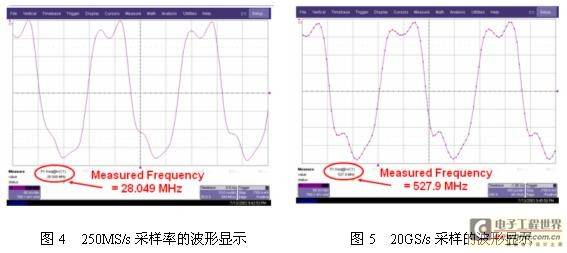
Therefore, in actual measurements, for higher frequency signals, engineers should always keep an eye on the oscilloscope's sampling rate to prevent the risk of aliasing. We recommend that engineers fix the oscilloscope's sampling rate before starting the measurement to avoid undersampling. LeCroy oscilloscopes provide this option in the Time Base menu for easy setting.

From the Nyquist theorem, we know that for an oscilloscope with a maximum sampling rate of 10GS/s, the highest frequency that can be measured is 5GHz, which is half of the sampling rate. This is the digital bandwidth of the oscilloscope, and this bandwidth is the upper frequency limit of the DSO. The actual bandwidth cannot reach this value. The digital bandwidth is derived from theory and is the theoretical value of the DSO bandwidth. It is completely different from the oscilloscope bandwidth (analog bandwidth) we often mention.

So in an actual digital storage oscilloscope, for a specific bandwidth, what sampling rate should be selected? It is usually related to the sampling mode used by the oscilloscope.

Sampling Mode
When the signal enters the DSO, all input signals need to be sampled before A/D conversion. Sampling techniques are generally divided into two categories: real-time mode and equivalent-time mode.

The real-time sampling mode is used to capture non-repetitive or single-shot signals, using fixed time intervals for sampling. After a trigger, the oscilloscope continuously samples the voltage and then reconstructs the signal waveform based on the sampling points.

Equivalent-time sampling is to sample a periodic waveform in different periods, and then splice the sampling points together to reconstruct the waveform. In order to obtain enough sampling points, multiple triggers are required. Equivalent-time sampling includes sequential sampling and random repeated sampling. Two prerequisites must be met to use the equivalent-time sampling mode: 1. The waveform must be repeated; 2. It must be able to trigger stably.
The bandwidth of the oscilloscope in real-time sampling mode depends on the maximum sampling rate of the A/D converter and the interpolation algorithm used. That is, the real-time bandwidth of the oscilloscope is related to the A/D and interpolation algorithm used by the DSO.

Here we mention the concept of real-time bandwidth, which is also called effective storage bandwidth. It is the bandwidth of a digital storage oscilloscope when it adopts real-time sampling. So many bandwidth concepts may drive you crazy. Let's summarize it here: the bandwidth of a DSO is divided into analog bandwidth and storage bandwidth. Usually, the bandwidth we often talk about refers to the analog bandwidth of the oscilloscope, that is, the nominal bandwidth on the oscilloscope panel. The storage bandwidth is the theoretical digital bandwidth calculated according to the Nyquist theorem, which is only a theoretical value.
Usually, we use effective storage bandwidth (BWa) to characterize the actual bandwidth of a DSO, which is defined as: BWa = maximum sampling rate / k. For a single signal, the maximum sampling rate refers to its maximum real-time sampling rate, that is, the maximum rate of the A/D converter; for a repetitive signal, it refers to the maximum equivalent sampling rate. K is called the bandwidth factor, which depends on the interpolation algorithm used by the DSO. The interpolation algorithms used by DSO generally include linear interpolation and sinusoidal (sinx/x) interpolation. K is about 10 when using linear interpolation and about 2.5 when using sinusoidal interpolation. However, k=2.5 is only suitable for reproducing sinusoidal waves. For pulse waves, k=4 is generally used. At this time, the effective storage bandwidth of a DSO with a sampling rate of 1GS/s is 250MHz. [page]

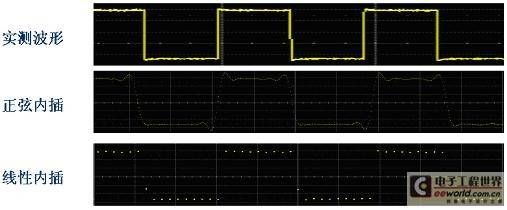
Figure 6 Waveform display of different interpolation methods

The theoretical relationship between interpolation and maximum sampling rate is not the focus of this article. We only need to understand the following conclusions: When using sinusoidal interpolation, in order to accurately reproduce the signal, the oscilloscope's sampling rate must be at least 2.5 times the highest frequency component of the signal. When using linear interpolation, the oscilloscope's sampling rate should be at least 10 times the highest frequency component of the signal. This also explains why the maximum sampling rate of an oscilloscope is usually four times or more of its rated analog bandwidth when used for real-time sampling.

After discussing the sampling rate, there is another concept closely related to the A/D of the DSO, which is the vertical resolution of the oscilloscope. The vertical resolution determines the smallest voltage increment that the DSO can distinguish, and is usually expressed by the number of bits of the A/D n. As mentioned earlier, the A/D converters of the current DSO are all 8-bit encoded, so the smallest quantization unit of the oscilloscope is 1/256 (2 to the 8th power), which is 0.391%. It is very important to understand this. For the voltage amplitude measurement, if the current vertical scale of your oscilloscope is set to 1v/div, it means that your measured value has an error within 8V*0.391%=31.25mV, which is normal! ! ! Because the voltage less than 31.25mV can no longer be distinguished by the oscilloscope at this gear. If only 4 bits are used, the measured error will be even more amazing! Therefore, it is recommended that when measuring the waveform, adjust the waveform as much as possible to make it fill the entire screen and make full use of the 8-bit resolution. We often hear engineers complain that the oscilloscope cannot measure his voltage accurately or the measurement results are inconsistent. In fact, in most cases, the engineers have not yet understood the impact of the oscilloscope's vertical resolution on the measurement results. By the way, regarding the measurement accuracy of the oscilloscope, one thing must be clarified - the oscilloscope itself is not a measuring instrument! ! ! It is the "engineer's eyes" to help you understand the characteristics of your circuit more deeply. Advertisement: Engineers who often do power supply measurement or ripple measurement, or want to have a deeper understanding of the quantization error of the oscilloscope, you can refer to an article on my colleague Frankie's blog "Oscilloscope is not a vertical measurement tool" http://blog.sina.com.cn/s/blog_521262a301009ryp.html
Figure 7 is a comparison of the measurement results at different sampling rates using an oscilloscope with an analog bandwidth of 1GHz to measure a pulse with a rise time of 1ns. It can be seen that a sampling rate of more than 5 times the bandwidth provides good measurement accuracy. Furthermore, based on our experience, we recommend that engineers ensure that there are more than 5 sampling points on the rising edge when measuring pulse waves. This ensures that the waveform is not distorted and improves measurement accuracy.

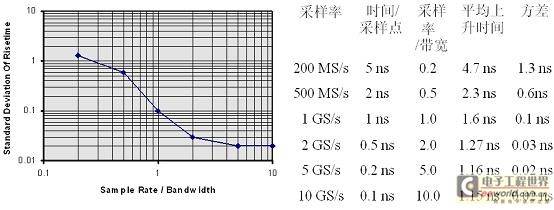
Figure 7 Relationship between sampling rate and bandwidth

Figure 8: Low sampling rate leads to waveform distortion

When talking about sampling rate, we cannot ignore the memory depth. For DSO, these two parameters are closely related.

Storage, storage depth The
storage of the oscilloscope is to store the eight-bit binary waveform information after A/D digitization in the high-speed CMOS memory of the oscilloscope. This process is called the "write process". The capacity (storage depth) of the memory is very important. For DSO, its maximum storage depth is fixed, but the storage length used in actual testing is variable.

When the storage depth is constant, the faster the storage speed, the shorter the storage time. There is an inverse relationship between them. The storage speed is equivalent to the sampling rate, and the storage time is equivalent to the sampling time. The sampling time is determined by the time represented by the display window of the oscilloscope. Therefore: Storage depth = sampling rate × sampling time (distance = speed × time).
The Time Base label of the LeCroy oscilloscope directly displays the relationship between the three, as shown in Figure 9.

Figure 9 Relationship between storage depth, sampling rate, and sampling time (time base) [page]

Since the horizontal scale of the DSO is divided into 10 grids, the length of time represented by each grid is the time base (time base), and the unit is t/div, so the sampling time = time base × 10. From the above relationship, we know that increasing the storage depth of the oscilloscope can indirectly increase the sampling rate of the oscilloscope: when measuring a waveform of a longer time, since the storage depth is fixed, it can only be achieved by reducing the sampling rate, but this will inevitably cause a decrease in the quality of the waveform; if the storage depth is increased, it can be measured at a higher sampling rate to obtain an undistorted waveform. The curve in Figure 10 fully reveals the relationship between the sampling rate, storage depth, and sampling time, as well as the impact of the storage depth on the actual sampling rate of the oscilloscope. For example, when the time base selects the 10us/div gear, the sampling time of the entire oscilloscope window is 10us/div * 10 grids = 100us. At a storage depth of 1Mpts, the current actual sampling rate is: 1M÷100us=10Gs/s. If the storage depth is only 250K, then the current actual sampling rate is only 2.5GS/s!

Figure 10 Memory depth determines the actual sampling rate

In a word, memory depth determines the DSO's ability to analyze both high-frequency and low-frequency phenomena, including high-frequency noise in low-speed signals and low-frequency modulation in high-speed signals.

After discussing the relevant theories of sampling rate and storage depth, let's take a deeper look at the impact of these two parameters on our actual tests in combination with common applications.

The Importance of Long Storage in Power Measurements

Since the frequency of power electronics is relatively low (mostly less than 1MHz), engineers who are used to using high-bandwidth oscilloscopes for high-speed signal measurements often have an illusion that power measurement may be simple. The fact is that many engineers make mistakes in choosing oscilloscopes for power measurement applications. Although the bandwidth of a 500MHz oscilloscope is sufficient for the power switching frequency of several hundred kHz, we often ignore the selection of sampling rate and storage depth. For example, in the test of common switching power supplies, the frequency of voltage switching is generally 200KHz or faster. Since there is often power frequency modulation in the switching signal, engineers need to capture a quarter cycle or half cycle of the power frequency signal, or even multiple cycles. The rise time of the switching signal is about 100ns. We recommend that in order to ensure accurate reconstruction of the waveform, there should be more than 5 sampling points on the rising edge of the signal, that is, the sampling rate should be at least 5/100ns=50MS/s, that is, the time interval between two sampling points should be less than 100/5=20ns. The requirement of capturing at least one power frequency cycle means that we need to capture a 20ms long waveform, so we can calculate the required storage depth of each channel of the oscilloscope = 20ms/20ns=1Mpts!!! Similarly, in analyzing the maximum value of the voltage stress borne by the power device during the soft start process of the power supply, it is necessary to capture the entire power-on process (more than ten milliseconds), and the required oscilloscope sampling rate and storage depth are even higher!

Unfortunately, I often see engineers using an oscilloscope with only 10K memory depth per channel to perform the above power supply test!!! This makes me feel more and more that as an oscilloscope manufacturer, it is necessary to devote more energy and time to help engineers establish the correct concept of using oscilloscopes. This is also the original intention of our Shenzhen office to write a series of articles.

The impact of memory depth on FFT results

In a DSO, the spectrum of a signal can be obtained through the fast Fourier transform (FFT), and then a signal can be analyzed in the frequency domain. For example, the measurement of power supply harmonics requires the use of FFT to observe the spectrum. In the measurement of high-speed serial data, FFT is often used to analyze the noise and interference that cause system failure. For FFT operations, the total amount of acquisition memory available to the oscilloscope will determine the maximum range (Nyquist frequency) in which the signal components can be observed, and the memory depth also determines the frequency resolution △f. If the Nyquist frequency is 500 MHz and the resolution is 10 kHz, consider determining the length of the observation window and the size of the acquisition buffer. To obtain a resolution of 10kHz, the acquisition time is at least: T = 1/△f = 1/10 kHz = 100 ms. For a digital oscilloscope with 100 kB of memory, the highest frequency that can be analyzed is:

△f × N/2 = 10 kHz × 100 kB/2 = 500 MHz

Figure 11 Oscilloscope FFT calculation [page]

In the example shown in Figure 12, a 266 MHz signal is affected by noise pickup from a 30 kHz noise source. The FFT (lower trace) shows a series of peaks centered at 266 MHz and spaced 30 kHz apart. This type of distortion is very common and can be caused by crosstalk from a switching power supply, DC-DC converter, or other source. It can also be caused by intentional use of spread spectrum clocking.

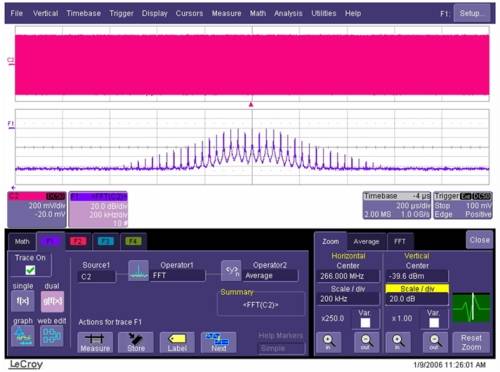
Figure 12 FFT analysis of LeCroy oscilloscope

For DSO, long memory can produce better FFT results, increasing both frequency resolution and signal-to-noise ratio. In addition, for some applications, some very detailed information can only be analyzed at a memory depth of 20Mpts, as shown in Figures 13 and 14.

Figure 13: The FFT result of 1M points cannot reveal information about modulation

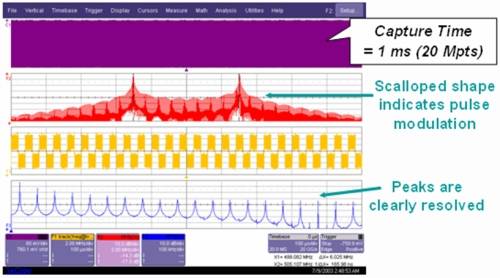
Figure 14 The 20M-point FFT clearly confirms the bimodal distribution of the clock and the related modulation rules

It should be pointed out that FFT analysis of long waveforms requires the oscilloscope to have super data processing capabilities, which often exceeds the computing limit of some oscilloscopes. LeCroy oscilloscopes can perform up to 25M points of FFT analysis, while the oscilloscopes of T Company in the industry can only perform up to 3.125M points of FFT analysis.

High-speed serial signal analysis requires truly long storage

Jitter analysis and eye diagram testing have become important means of analyzing high-speed serial links and an important reference for evaluating high-end oscilloscopes.

When using an oscilloscope for jitter testing, the high-speed acquisition memory length is a key indicator for the oscilloscope to perform jitter testing. The high-speed memory length not only determines the number of samples in a jitter test, but also determines the jitter frequency range that the oscilloscope can test. This is because all jitter has different frequency components, which usually range from DC to high frequency. The reciprocal of the oscilloscope's single acquisition time window indicates the frequency range of the jitter test. For example, if you use an oscilloscope with a sampling rate of 20G samples/second (S/s) and 1M sampling memory to capture a 2.5Gbps signal, then your oscilloscope screen can capture a 50 microsecond long waveform, which means that you can capture a low-frequency jitter cycle with a frequency of 20kHz. Similarly, for a 20GS/s sampling rate and 100M memory depth (such as LeCroy's SDA6000AXXL), you can capture a low-frequency jitter cycle of 200Hz.

Traditional oscilloscopes are designed to physically implement the high-speed acquisition front end (up to 80 ADCs) and high-speed memory on a single SoC chip. Since there are too many functions inside a chip, the capacity of the on-chip high-speed memory is limited (generally less than 2M at 40GS/s), and only jitter above 20KHz can be measured. When low-frequency jitter needs to be tested, the memory cannot be expanded or upgraded. For most applications, it is very important to test and analyze jitter information in the range of 200Hz to 20KHz. In order to make up for the defects of this design structure, this type of oscilloscope will use external low-speed memory to make up for the on-chip high-speed memory, but the external memory cannot work at a high sampling rate and generally can only provide 2GS/s, and cannot provide meaningful jitter test results. For example, when using 40GS/s real-time high-speed acquisition, the 512K memory can only collect 12.5us of data at a time, and can only test jitter with a frequency range of more than 80K. It is difficult to meet the test requirements in various serial bus and clock jitter tests.

In the eye diagram test, since the software clock recovery (CDR) technology pioneered by LeCroy has become the industry standard, in today's era of high-speed serial buses, oscilloscopes need to have stronger data processing capabilities to perform real-time eye diagram analysis on a large number of data samples. For example, the eye diagram analysis of PCIE-G2 and other devices requires the measurement of 1 million UI data at a time. Not all manufacturers' oscilloscopes can perform real-time and dynamic eye diagram measurements on all captured data samples like LeCroy oscilloscopes.



Figure 19 The result of an eye diagram of 494.046K data captured at one time by a LeCroy oscilloscope