Design method of missile decoupling controller based on H∞ mixed sensitivity

1 Introduction
When a missile flies at a high angle of attack, there is serious aerodynamic coupling between channels. In engineering design, smaller coupling terms are usually treated as random interference. However, when the coupling effect is large, the control system will easily lose stability. Therefore, the coupling effect between channels must be considered and decoupled. In recent years, with the development of control theory, a variety of decoupling control methods have emerged, such as characteristic structure configuration decoupling, self-correction decoupling, linear quadratic decoupling, singular perturbation decoupling, adaptive decoupling, intelligent decoupling, H∞ decoupling, variable structure decoupling, etc. Among them, reference [4] uses a multivariable frequency domain method to transform the coupled MIMO system into a series of SISO systems, and then uses the classical frequency domain method to design them separately, realizing the decoupling of the BTT missile autopilot. Reference [5] uses the output feedback characteristic structure configuration method to reasonably configure the eigenvalues ​​and eigenvectors of the closed-loop system, obtain the output feedback and feedforward controllers, and realize the decoupling of the three channels of the missile. Reference [6] uses variable structure control and robust control to realize the dynamic decoupling of the system.
During the flight of a missile at a high angle of attack, the missile is subject to very large parameter uncertainties and external interference. It is difficult to ensure the real-time requirements of the control system using general decoupling methods. Due to the advantages of H∞ mixed sensitivity itself, a design method based on H∞ mixed sensitivity decoupling controller is proposed here. The H∞ mixed sensitivity decoupling controller involves the ideal uncoupled closed-loop system in the mixed sensitivity design to achieve the purpose of decoupling. In the design of the H∞ mixed sensitivity controller, it is necessary to select the weight function to achieve the purpose of decoupling. The advantage of this decoupling control method is that due to the advantages of the H∞ mixed sensitivity controller itself, the decoupling controller has strong robust stability and anti-interference ability.

2 Simplified mathematical model of high-angle-of-attack reentry missile
The dynamic characteristics of the missile are described by a set of nonlinear, variable-coefficient equations. Due to the influence of factors such as elastic vibration, liquid sloshing and engine swing, the equations are very complex. In order to facilitate various analyses, calculations and missile control system designs of the missile motion equations, this paper adopts small perturbation simplification measures. Considering the rigid body motion and elastic vibration of the missile, assuming that the standard ballistic parameters of the yaw and roll channels are zero, the following missile body motion equations based on the small perturbation assumption are obtained. The small perturbation missile body motion consists of the rigid body attitude motion equation and the elastic vibration equation. Equations (1) to (3) are simplified mathematical models.
(1) Pitch-normal channel rigid body motion equation:

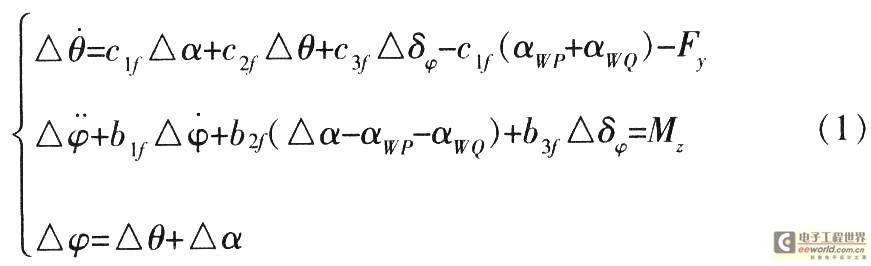
In the equation, αWP, αWQ are the additional angles of attack formed by the steady wind and shear wind, respectively; My, Mx are structural disturbance torques; δ is the trajectory heading angle; β is the trajectory sideslip angle; ψ is the trajectory yaw angle; δψ is the actual trajectory yaw rudder deflection angle; Fx is the structural disturbance force.
(2) Rigid body motion equation of the yaw-transverse channel:

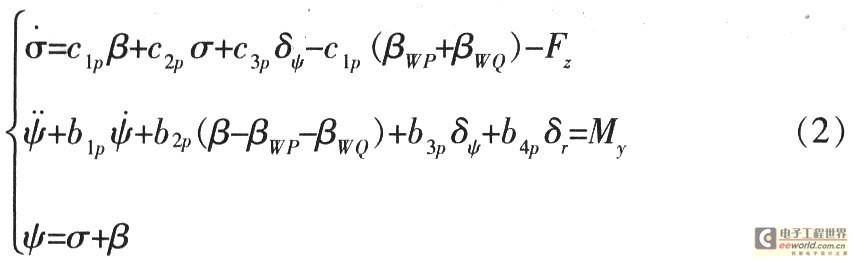
In the formula, βWP and βWQ are the additional sideslip angles of the missile due to the steady wind and shear wind respectively; qiψ is the generalized coordinate corresponding to the i-th vibration mode (excluding rigid body vibration mode) of the yaw-transverse channel.
(3) The motion equation of the missile body in the rolling channel:

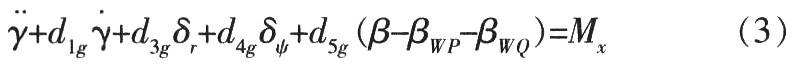
In the formula, γ is the ballistic rolling angle; δr is the ballistic rolling rudder deflection angle.

3 Mathematical model of coupled missile
From the simplified model of the above three channels, it can be seen that the missile motion equation of the yaw channel contains the parameters of the rolling channel (δ, γ), and the missile motion equation of the rolling channel contains the parameters of the yaw channel (δ, ψ, β). The mutually coupled pitch-normal channel (1), yaw channel (2) and rolling channel (3) are combined to form a multivariable system with two inputs and two outputs. The state vector is [β ψ ψ γ γ]T, the control input is u=[δψc δγc]T, and the measurement output is r=[ψc γc]T. The state space expression of the missile motion equation is obtained as follows:

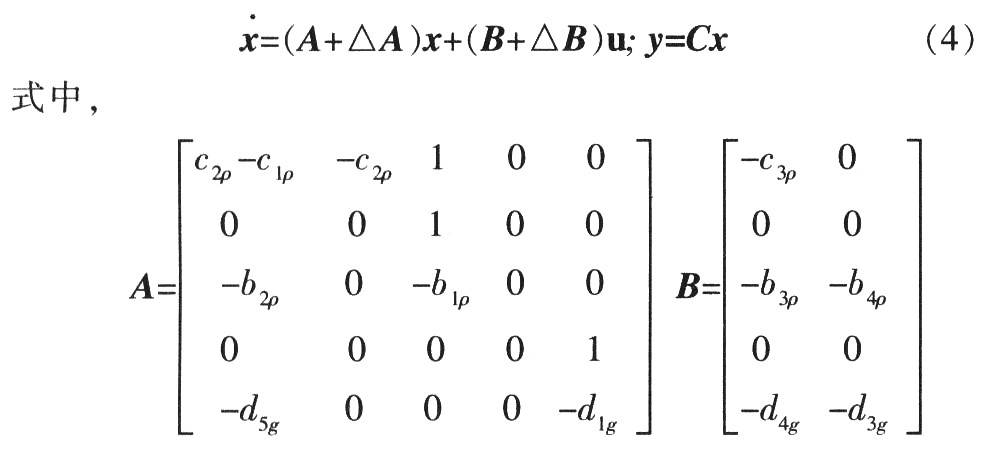
△A, △B are the parameter uncertainties caused by high-frequency elastic vibration, etc., and 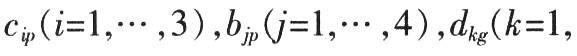2, 3, 4) are coefficients.

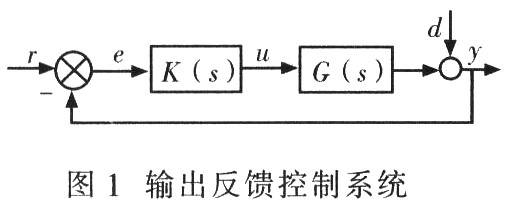
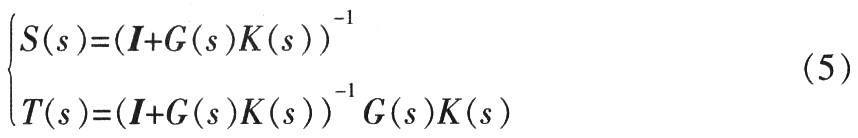
From formula (5), we know that S(s)+T(s)=I, where I is the unit matrix. Select an appropriate weighting function to perform frequency domain shaping on S(s) and T(s), that is, in the low frequency band, the gain of the sensitivity function is mainly reduced, and in the high frequency band, the gain of the complementary sensitivity function is mainly reduced, so that the system satisfies the following after frequency domain shaping:

In the formula, Ws(s) is the weighted performance reflecting the system's anti-interference ability, and WT(s) is the weighted performance reflecting the system's robustness.
4.2 Decoupling controller design problem
From formula (5), we can see that T(s) is the closed-loop transfer function of the system shown in Figure 1. To this end, T(s) can be shaped into an ideal diagonal matrix to achieve the purpose of decoupling. Reference [4] gives a method to shape H∞ mixed sensitivity into a standard H∞ problem. This paper derives it on this basis and selects an appropriate weighting function to achieve the purpose of decoupling. Figure 2 is a block diagram of H∞ mixed sensitivity. In Figure 2, z1 and z2 are performance evaluation outputs. uS and uT are the inputs of Ws(s) and WT(s), respectively, and yG is the output of G(s).

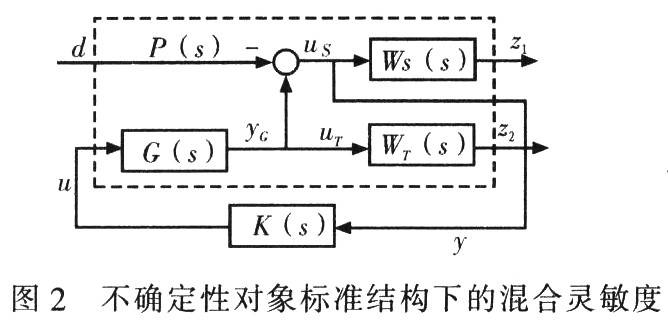
Then the state space realizations of G0(s), WS(s), and WT(s) are:

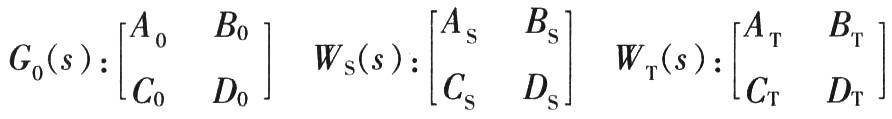
As shown in Figure 2, the input of system P(s) is d,u, and the output is z1,z2,y. Let x0,xS,xT be the output states of G(s),WT(s),WS(s). From Figure 2, we can deduce that:yG=C0x0+D0uyuT=yg,us=d-yG, then:

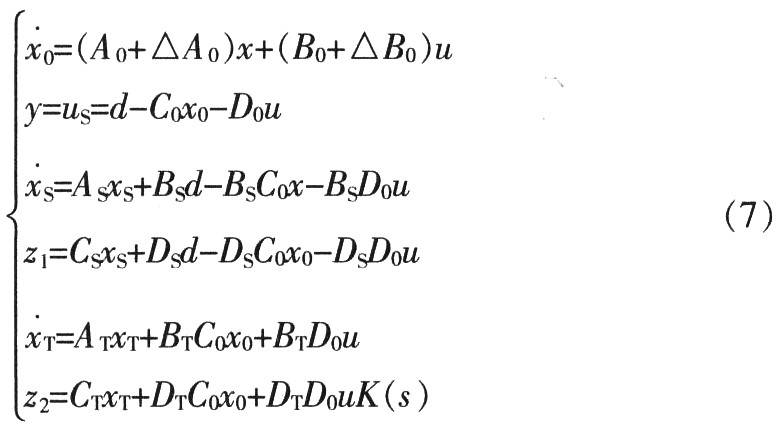
Assume x = [x0 xS xT]T, z = [z1 z2]T, define the virtual output signal zp = F1x + F2dF3u, the virtual input signal dp = zp, and consider equation (7), the realization of the expanded state space of the generalized object P(s) is obtained as follows:

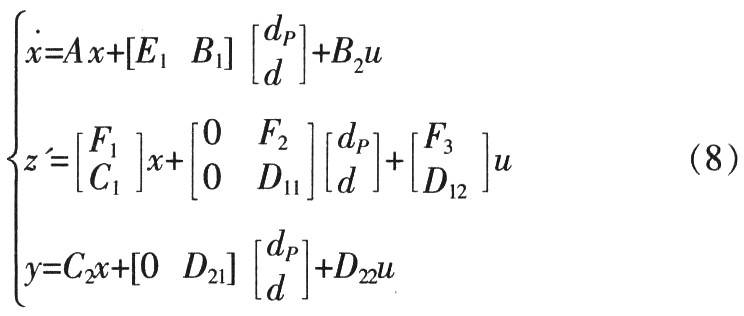
In equation (8), the parameter uncertainties △A, △B1 and △B2 should satisfy the following relationship:

In this way, the robust controller design problem of uncertain systems is transformed into the H∞ standard design problem.
It can be seen from the H∞ standard design problem that the selection of weighting functions WS(s) and WT(s) is involved here. Considering the decoupling invariance of the system, WS(s) and WT(s) should be diagonal matrices in the following form:

Where WSj(s), WTj(s)(j=1,…,m) are

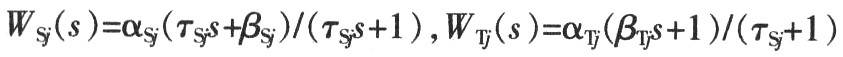
4.3 Principles for selecting weighting functions
Perform frequency domain shaping on S(s) and T(s). In the low frequency band, the gain of the sensitivity function is mainly reduced, while in the high frequency band, the gain of the complementary sensitivity function is mainly reduced. In the low frequency band, S(jω) is made below the gain curve VS(jω), while in the high frequency band, T(jω) is made below VT(jω).

5 Simulation Example
Taking a certain aircraft as an example, under certain flight conditions, the tracking model of the two channels is Where:

According to the conditions satisfied by the sensitivity function S and the complementary sensitivity function T in equation (5) and equation (6), and the selection principle of equation (10) and weighting function, the sensitivity function and the weighting function of the complementary sensitivity Ws(s), WT(s) can be obtained:

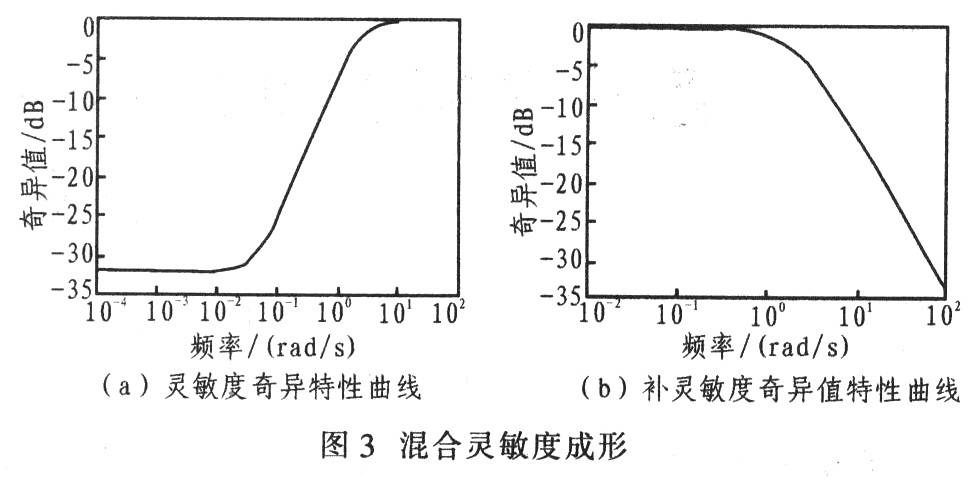
By simulating it, frequency domain shaping is performed, and the mixed sensitivity is formed as shown in Figure 3. It can be seen from Figures 3a and 3b that by appropriately selecting the weighting function, frequency domain shaping is performed on S and T. The singular values ​​of the sensitivity and complementary sensitivity singular value curves in the full frequency band are all smaller than the singular values ​​of the inverse of the weighting function matrix, which meets the singular value requirements and also meets the requirements of equation (6), which can make the system have good robustness and anti-interference ability, meet the decoupling conditions of the system, and achieve the decoupling purpose.

6 Conclusions
Aiming at the situation that the yaw channel and the roll channel have large coupling during the missile reentry at a high angle of attack, the H∞ mixed sensitivity decoupling control method is used for decoupling, and the weighting function based on the mixed sensitivity decoupling controller is selected so that the weighting function can better take into account the complementary sensitivity shaping and system decoupling, thereby overcoming the conservatism in the system design. The simulation results show that the decoupling method can make the system have good decoupling and robust stability.