Research on Digital PID Control Method of DC/DC Converter

1 Introduction

With the emergence of digital signal processors such as DSP, digital control of power electronic circuits has made great progress. Digital processors can instantly read the output value of the converter and quickly calculate the control value to control the converter. Since digital control can adopt flexible control strategies, it is possible to apply some advanced control methods to power electronic circuits. As the price of digital processors continues to decline and the performance continues to improve, the number of switch-type power conversion devices using digital control will increase day by day. The future development direction of power electronics can be summarized as "high frequency, digitalization, greening, and modularization."

PID control is one of the earliest developed control strategies. Due to its simple algorithm, good robustness and high reliability, it is widely used in various controls, especially for deterministic systems that can establish accurate mathematical models. However, the actual power electronic system is a system that combines linear and nonlinear, and it is difficult to establish an accurate mathematical model. In the actual debugging process, PID parameters are often poorly adjusted, performance is poor, and adaptability is relatively poor. For a long time, people have been seeking a method to adjust digital PID parameters. According to the hardware conditions of the converter system, this paper adjusts the sampling frequency to the limit value to improve the control performance of the system, uses the pole configuration method to adjust the proportional, integral, and differential coefficients of PID, and revise these parameters through MATLAB simulation to obtain good control effects.

2. Introduction to Control Object

The object of this paper is the phase-shifted full-bridge zero-voltage switching converter. The main circuit is shown in Figure 1. This converter combines the advantages of zero-voltage quasi-resonant technology and traditional PWM converter technology. The operating frequency is fixed. During the commutation process, LC resonance is used to make the device zero-voltage switch. After the commutation is completed, PWM technology is still used to transmit energy. The switching loss is small and the reliability is high. It is a soft switching circuit suitable for large and medium power switching power supplies.

Figure 1 Phase-shift controlled full-bridge converter

The controller is Motorola's DSP chip 56F8323, with a switching frequency of 150kHz, and uses a single-loop control of output voltage. The voltage loop sampling frequency is 25kHz. In the voltage loop, the output voltage is sampled and the output voltage deviation and deviation change are calculated to complete the PID calculation of the voltage loop, and at the same time complete functions such as overvoltage protection. The calculation result is used as the basis for the size of the phase shift angle to realize the control of the converter.

Here, in order to establish a simple mathematical model of a DC/DC converter that does not depend on the specific load type, the following assumptions are made:

①The power switch tube is an ideal device;
②LC forms a low-pass filter;
③The high-frequency transformer is an ideal transformer;
④Taking into account the damping factors such as the on-state voltage drop of the switch tube, the dead zone effect, the line resistance and the equivalent series resistance of the filter inductor, an equivalent resistance is synthesized as r.

3 Comparison of two digital PID control methods

Digital control is a sampling control, which can only calculate the control quantity according to the deviation value at the sampling time, so the integral term and the differential term need to be discretized. Using a series of sampling time points kT to represent the continuous time t, replacing the integral with the sum, and replacing the differential with the increment, the discrete position PID expression can be obtained:

The flow of the position PID control algorithm is shown in Figure 2.

Figure 2 Flowchart of position PID control algorithm

Figure 3 Flowchart of incremental PID control algorithm

When the actuator needs to increase the control quantity, the incremental PID control algorithm can be derived from equation (1), as shown in equation (2). The incremental PID control algorithm flow is shown in Figure 3.

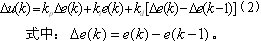
The position algorithm is a full output, and each output is related to the past state. When calculating, e(k) must be accumulated, and the digital processor has a large amount of calculation. Moreover, once a problem occurs, the output amplitude of the controller will be very large, which will cause the actuator to change drastically. This situation should be avoided. The incremental algorithm does not have this problem. It is an incremental output, and there is no need to accumulate the past state, so the impact of false operation is small. The incremental algorithm also has shortcomings and has static errors. Therefore, if the accuracy requirements are high and the action is relatively fast, the position algorithm is used, such as the control of the power electronic converter in this article; if the execution time is relatively long, such as motor speed control, etc., the incremental algorithm is selected. In order to overcome the shortcomings of the position algorithm in this article, anti-integral saturation is introduced, and a limit range is set to avoid large changes in the controller amplitude.

4 DC/DC converter digital PID parameter setting

4.1 Determination of sampling frequency

Sampling frequency is a very important parameter in digital control systems. From the perspective of signal fidelity and control performance, the higher the sampling frequency of the converter system, the better. The higher the sampling frequency, the higher the hardware requirements, which increases the hardware cost. Therefore, a compromise method should be adopted to select the best sampling period when selecting the sampling period.

Figure 4 Diagram of judging the end of program execution

The digital controller used in this paper is the MC56F8323 chip of Freescale, with a main frequency of 60MHz. In order to determine the maximum sampling frequency that the converter system can achieve under the existing hardware conditions, a general input and output port is used at the beginning of the interrupt program to give a level flip indication signal, and the sampling frequency is continuously increased. The interrupt program can be judged whether it can be executed according to the flip signal. If the indication signal frequency is less than half of the sampling frequency, as shown in the last case of Figure 4, it means that the real-time interrupt cannot be completed within the specified time, which is the maximum allowable sampling frequency of the system under the existing conditions. Different algorithm programs have different maximum sampling frequencies that the converter system can achieve.

4.2 Pole configuration to select PID parameters

Although the digital control system is a discrete system, if the sampling period T is small enough, the digital control system can be approximately regarded as a continuous system. After the control parameters of the continuous system are discretized, the digital controller can realize the regulation of the converter.

According to the above assumptions, when the cutoff frequency of the converter's LC output filter is much smaller than the switching frequency and the DC bus input voltage Uin remains constant, the phase-shifted full-bridge converter can be regarded as a constant-gain amplifier except for the output filter part. The s-domain model of this part is shown in Figure 5.

Figure 5 S-domain model of the phase-shifted full-bridge main circuit

In Figure 5, Uab(s) is the voltage after secondary rectification, and Uc(s) represents the output value of the controller. Here, several quantities are set, iL represents the inductor current, and io represents the load current. For the convenience of analysis, io is regarded as the disturbance of the load.

Considering the disturbance of the output voltage and load current after rectification of the phase-shifted full-bridge converter, the output response of the output filter is derived using the state space average model method, as shown in equation (3). At the same time, a block diagram can be drawn as shown in Figure 6.

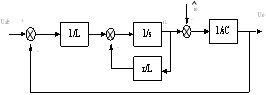
Figure 6 S-domain model of the output filter

Combining the main circuit, filter and PID controller models, the system block diagram can be obtained as shown in Figure 7.

Figure 7 PID controlled DC/DC converter system block diagram

According to Figure 7, the closed-loop transfer function of the system can be obtained, see equation (4).

The three roots of the characteristic equation (5) are the three closed-loop poles of the system transfer function. The dynamic response performance and stability of the closed-loop system are mainly determined by the position of the closed-loop poles on the s-plane. The closed-loop system of the phase-shifted full-bridge DC/DC converter is a third-order system, which belongs to a high-order system. Its dynamic characteristics are mainly determined by the closed-loop dominant poles. If the closed-loop system dominant poles are determined to be located at, according to the dynamic performance indicators of the converter control system , where Wr and Wr are the desired damping ratio and natural frequency, respectively, then the closed-loop non-dominant poles of the system can be selected , n is a positive constant, and the larger the value of n, the closer the response characteristics of the third-order system determined by the three closed-loop poles are to the second-order system determined by the closed-loop dominant poles, generally n=5~10. The characteristic equation of the closed-loop system that meets the dynamic performance requirements is obtained as follows:

By comparing equation (5) and equation (6), the required parameters can be obtained. This equation is obtained by the pole configuration method, so it is called the pole configuration PID parameter formula.

The specific parameters of the actual circuit of the phase-shifted full-bridge DC/DC converter in this paper are: input Uin=140V~200V, output U0=24V, output power P=220W, output filter inductor L=20μH, output filter capacitor C=2200μF. In the above model, the value of the equivalent resistance r is difficult to estimate through theoretical analysis. Considering that kp and ki are not affected by r, r=0.264 is taken according to experience. Determine the desired damping ratio and natural frequency Wr. According to the step response curve of the second-order system, it can be known that the smaller the damping ratio, the shorter the rise time, and the overshoot of the system also increases. When it is small to a certain extent, the system will oscillate. Observing the step response curve from 0 to 1, it is found that the damping ratio is preferably between 0.4 and 0.8. At this time, the rapidity and oscillation of the unit step response are taken into account. According to a large amount of engineering experience, =0.707 is the best damping ratio, so 0.707 is selected in this paper. The selection of Wr is determined by the damping ratio and the adjustment time required by the system. In this paper, Wr is selected as 1600rad/s. Based on the above parameters, kp=0.24, ki=1274, and kd=0.0000165 are obtained.

5 Simulation and Experimental Results

This paper adopts single voltage loop control to measure the steady-state output voltage and output current at light load of 24W and heavy load of 216W, and simultaneously conducts sudden loading experiment from 24W to 216W and sudden unloading experiment from 216W to 24W.

FIG8 shows the steady-state output voltage and current waveforms when the input voltage is 150V and the output power is 216W.

Figure 8 Steady-state voltage and current output waveform

Figure 9 shows the output voltage and current waveforms when the output power increases from 24W to 216W with a sudden load. When the load is suddenly increased, the voltage drops by 4.8V, the overshoot is 20%, and the adjustment time takes 20ms.

Figure 9 Po: 24W→216W voltage and current output waveform

Figure 10 Po: 216W→24W voltage and current output waveform

Figure 10 shows the output voltage and current waveforms when the output power drops from 216W to 24W when the input voltage is 150V. When the load is suddenly unloaded, the voltage overshoots by 2.16V and the overshoot is 9%. The adjustment time is 25ms.

6 Conclusion

The experimental operation shows that DSP meets the hardware requirements of the position-based digital PID control algorithm, and the maximum sampling frequency obtained through testing improves the control performance of the system. The parameters obtained by the pole configuration method meet the system requirements and have good static and dynamic characteristics.