Spectrum Analysis Based on Space Electromagnetic Signals

    The battlefield electromagnetic environment has a profound impact on war preparations and various military activities, especially on battlefield perception, command and control, combat operations, weapon effectiveness, battlefield construction, etc. Under information conditions, the battlefield electromagnetic environment has unpredictable complexity and unpredictability. There are many elements that constitute the battlefield electromagnetic environment, but human electromagnetic activities are the most active factor. The electromagnetic environment is invisible and cannot be intuitively felt. Analyzing its composition and characteristics is crucial to understanding the battlefield electromagnetic environment. Therefore, the analysis of space electromagnetic signals and intensity has become an important research topic. In the analysis of space electromagnetic signals and intensity, spectrum analysis is indispensable.
    In this paper, the theory and implementation method of space electromagnetic signal spectrum analysis are proposed for the electromagnetic environment of the actual battlefield, and the relationship between signal sampling, signal time domain and frequency domain is explained. Simulation experiments are carried out on the methods involved in this paper to verify the correctness and effectiveness of the proposed methods. The spectrum analysis of space electromagnetic signals and its implementation method proposed in this paper provide an analysis and experimental method close to the actual electromagnetic environment for the offensive and defensive sides of electronic warfare to conduct confrontation implementation and confrontation effectiveness evaluation.

1 Time-frequency relationship of signal
1.1 Sampling theorem
    Assume that the frequency range of the signal is [fL, fH]. According to the Nyquist sampling theorem, the sampling frequency must be greater than 2 times the highest frequency of the signal to ensure that the signal does not alias in the frequency domain. However, since radar signals often transmit signals with very high center frequencies, such as 10 GHz, and the bandwidth of the transmitted signal is generally in the MHz range, if the sampling is 2 to 3 times the center frequency according to the Nyquist low-pass sampling theorem, it will cause a great burden on the system.
    For this reason, the bandpass sampling theorem is adopted. Assume that the bandpass signal can accommodate m frequency shifts within the range of [-fL, fH] without generating spectrum aliasing.
   
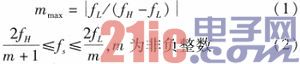
1.2 Spectral characteristics after bandpass sampling
    Assume that the center frequency of the signal is fc; the bandwidth is B. Figure 1 is the spectrum graph using the low-pass and bandpass sampling theorems respectively.

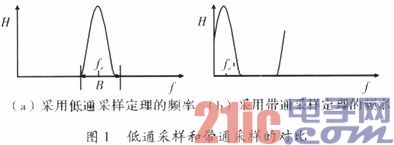
    Experiments have found that after the bandpass sampling theorem is adopted, the spectrum is shifted, and the center frequency is no longer fc on the spectrum diagram, but other values, but the spectrum shape and bandwidth remain unchanged.
    The relationship between the frequency after bandpass sampling and the frequency of the original signal is
   
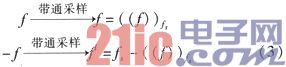
    : where f is the original frequency; fl is the corresponding frequency on the spectrum diagram after bandpass sampling;
((n))N represents n modulo N.
1.3 Relationship between signal amplitude and power
    Suppose the time domain form of the signal is x(t); the signal duration is τ, and the signal is sampled at fs to obtain a discrete signal of N points. Then the relationship between time, sampling frequency and number of points is
    τ=N／fs (4)
    Perform point FFT on the discrete signal x(n), that is, obtain the spectrum of the signal. Suppose the spectral line value at each point is H(n). Since the value on each spectral line of FFT is the superposition of N points of Fourier transformation, the spectrum after FFT transformation needs to be normalized, so the power of the signal is

    If it is a two-dimensional signal, since the signal has real and imaginary parts, the relationship between amplitude and average power is P=A2
[page]

2 Time Domain Form and Power of Space Electromagnetic Signals
2.1 Power of Electromagnetic Signals in Free Space
    Electromagnetic signals in space are complex and diverse. Taking the radar that most often appears in space combat as an example, the electromagnetic signals in free space are calculated. According to the radar equation, the power of the radar signal at a receiving point in space is where
   
    Pt and Gt represent the radar's transmitting power and transmitting antenna gain respectively; σ represents the cross-sectional area at the receiving point in space; R represents the distance between the radar and the target point; Lr represents the total system loss of the radar. Where σ=, so the power is where
   
    Gr is the receiving antenna gain at the receiving point; λ is the wavelength of the transmitted signal.
2.2 Time Domain Form of Electromagnetic Signals
    Assume that there are multiple radars in space, where the position vector of each radar is Lri, and the transmitted signal is sr(i, t), where i represents the serial number of the radar, and i=1,…,M.
    According to the relationship between signal amplitude and power, the amplitude of the i-th radar transmitter reaching the test point is where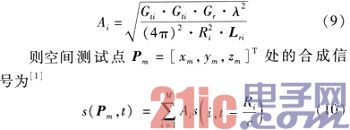

    Ri represents the distance between the i-th radar transmitter and the test point Pm; c represents the speed of light; and Ri/c represents the transmission delay between the observation point and each transmitter.
2.3 Power of electromagnetic signal
    Perform N-point FFT on the time domain signal s(Pm, t) to obtain the spectrum of the electromagnetic signal. The spectrum is calculated for the receiving frequency band according to formula (5) to obtain the signal power received at the receiving point.
However, this spectrum is the spectrum after being moved according to formula (5), and the spectrum needs to be restored. In the process of restoration, it is found that it is easier to calculate the power by moving the receiving frequency band, so the following method is used for calculation:
    (1) Move the receiving frequency f and calculate the frequency fl of the receiving frequency in the spectrum.
    (2) Calculate the spectral line position of fl in the spectrum and read the spectral line value at this point in the spectrum.
    (3) Multiply the spectral line value by the filter coefficient, normalize it and take the square.
    (4) Traverse the receiving frequency band and add the values ​​in formula (3) to obtain the receiving power.

3 Spectrum analysis of electromagnetic signals
    To verify the correctness of the proposed algorithm model and implementation method, VC software was used for software programming and simulation experiments, and Matlab was used to display the calculated results. Taking
    radar as an example, the radar information is as follows:
    radar position: longitude and latitude (119.5°, 19.5°, 100 m); azimuth scanning range (0°, 180°); elevation scanning range (30°, 90°); transmission center frequency 2.5 GHz; bandwidth 10 MHz; transmission power 50 kW; signal simulation duration 5 μs; transmission waveform: linear frequency modulation signal; set the receiving center frequency at the receiving end to 2.5 GHz; bandwidth 10 MHz.
    Through system simulation calculation, the sampling frequency fs=20040 080.32 and the number of sampling points N=1 024 are obtained. The
    calculated spectrum information is written into a file, and the waveform obtained by drawing with Matlab is shown in Figures 2 and 3.

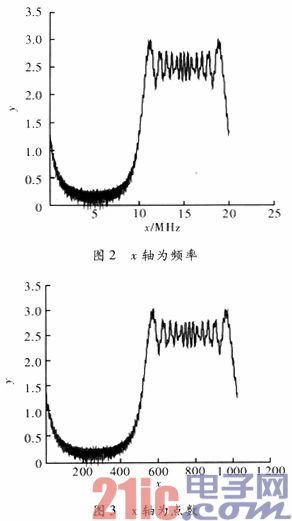
     By using formula (3), the center frequency is shifted to obtain ((fc))fs=((2 500 000 000))20040 080.32=15 030 080, which is consistent with the center frequency in Figure 1.

[page]

    By calculating step (2) in Section 2.3, we get the point position m = , which is consistent with the center frequency point position in Figure 2.
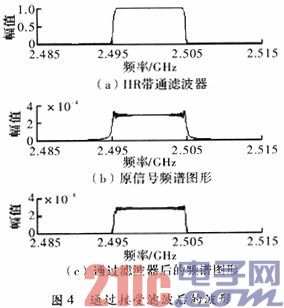
    Pass the spectrum through the filter and shift the spectrum of the filter according to formula (3), and we get the result shown in Figure 4. It can be seen that the test result is consistent with the input.

    Taking radar information as an example, the method in this paper is used to calculate the electromagnetic intensity of a region in space and test the results.
    Assume that the region is in the longitude range (119-120), the latitude range (19-20), and the altitude is 10000 m.

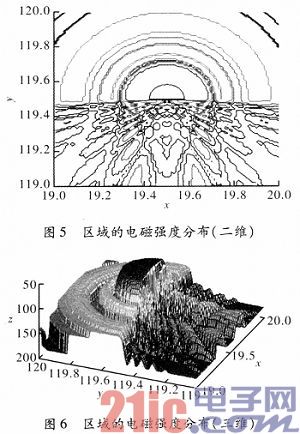
    The simulation results are shown in Figures 5 and 6. It can be seen that the azimuth scanning range is (0-180), which matches the input azimuth information, and the spatial intensity of the area covered by the main lobe of the radar antenna is significantly larger, and the lobe is obvious. This verifies the correctness of signal generation and spectrum analysis.

4 Conclusion
    For electromagnetic signals in space, their generation and spectrum analysis, as well as the sampling frequency, number of sampling points, spectrum shifting, and the relationship between power and spectrum are explained, and the correctness of the proposed method is verified through simulation. This helps to understand the complex electromagnetic environment and intensity analysis in space.