Relationship and calculation of various inductances of permanent magnet DC motor

In the control of permanent magnet DC motors, various coordinate transformations are often used, and various inductances are also encountered, such as phase inductance, line inductance, direct-axis inductance, quadrature-axis inductance, phase-to-phase mutual inductance, etc., especially when inductance and coordinate transformation are combined, many people are easily confused. Below we use pictures, texts and formulas to understand the relationship between DC motor inductance.

Inductance: In 1824, Oersted discovered the electric current effect. The magnetic needle around the current-carrying conductor will deflect, which is electricity generating magnetism. Later, Faraday and Henry discovered that magnetism can also generate electricity. The moving magnetic field can induce current in the conductor. This is what we now call electromagnetic induction. The mathematical engineering formula is:

e: Induced voltage

dф/dt: rate of change of magnetic flux (unit: Wb/s)

Shortly after Faraday published his paper on electromagnetic induction, Lenz discovered the law that determines the direction of the induced current, which is Lenz's law: the magnetic field of the induced current always hinders the change of the magnetic flux that causes the induced current, so the complete mathematical formula is:

Self-inductance and mutual inductance in DC motor control

In Abe's law: The fundamental reason for the generation of magnetic field is electric current (it can be the current in the conductor or the current in the permanent magnet). As shown in the figure below, when a coil is energized, a magnetic field will be generated.

The coil itself is in the magnetic field generated by itself, which means that magnetic flux will also be generated in the coil. This quantity is not intuitive for us and is not easy to measure. Since the magnetic flux is generated by the current, we can use the current to represent it, so the definition of inductance is:

The unit is Henry, an American physicist. He actually discovered the phenomenon of electromagnetic induction independently almost at the same time as Faraday, but Faraday published his results earlier and won the naming rights.

What we usually call inductance should strictly be called self-inductance, that is, the ability of the coil to generate magnetic flux on itself.

Since there is self-inductance, there will be mutual inductance, that is, the ability of two coils to generate magnetic flux between each other.

In DC motors, inductance is very important. It expresses the ability of current to generate a magnetic field in a specific mechanism. Once the inductance is determined, we can easily study the properties of the magnetic field.

What is magnetomotive force?

The definition of inductance is defined by magnetic flux. To calculate the inductance of a coil, we must first calculate the magnetic field generated when the coil is energized, and then calculate the magnetic flux. For example, the magnetic circuit in a DC motor is linear, the hysteresis and eddy current losses in the core can be ignored, and the subharmonics of the air gap magnetic field can also be ignored. The stator and rotor surfaces of the DC motor are smooth, and the effects of teeth and slots can be corrected by the Cartesian coefficient. The air gaps of the direct axis and the quadrature axis can be different, but the relative permeability of the air gap can be expressed by the average value plus the second harmonic.

The figure above shows the situation of the two-pole full-pitch coil in the stator slot of a DC motor. ⊙ is outflow and is inflow. According to Ampere's circuit theorem, the magnetomotive force distribution diagram is:

The magnitude of the magnetomotive force is

Performing Fourier series analysis on the square wave shows that it can be composed of 1st, 3rd, 5th, ... odd harmonics, among which the 1st harmonic is also called the fundamental wave, and its amplitude is:

The above analysis is about one pair of poles. Now assume that there are p pairs of poles and the total number of turns of each phase winding is Nph. Then the fundamental amplitude of phase A is:

In the above analysis, the windings are considered to be full pitch, and there is only one slot per pole per phase. This is rarely the case in actual motors. Most motors have multiple slots per pole, and they are short pitch:

We generally use a winding factor kω1 to correct the fundamental magnetomotive force, and its amplitude is:

Calculation of Phase Inductance and Mutual Inductance of DC Motor

According to the amplitude of the fundamental magnetomotive force, its distribution along the stator is:

With the magnetic potential, if we know the permeance (the inverse of the magnetic resistance), we can calculate the air gap flux density. For surface mounted DC motors, the air gap is basically unchanged, so the permeance has nothing to do with the position of the DC motor rotor; but for DC motors, the air gap changes along the circumference of the rotor (the change period is twice the number of pole pairs), so the permeance is also related to the rotor position.

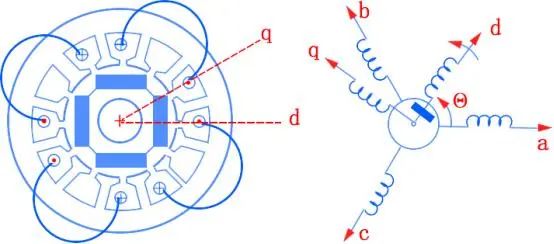
Since the dq axis is defined on the DC rotor, we can indicate the position of the rotor by the angle θ between the d axis and the A-phase winding.

Calculate phase inductance

The air gap specific permeability is:

λ(a)=λδ0+λδ2cos2(a+θ)

In the formula, because the air gap length change period is twice the pole pair number, there is a quadratic component, and when the DC motor type is embedded, λδ2 is a negative value, that is, the magnetic resistance is the largest and the magnetic permeance is the smallest on the d-axis.

The phase relationship between the air gap magnetomotive force and the specific permeance is:

The air gap flux density is the magnetomotive force multiplied by the specific permeance:

Bδ(a)=Fa1cosa·(λδ0+λδ2cos2(a+θ))

Expanded into the form of harmonic superposition:

So the fundamental air gap flux density is:

Then the magnetic flux corresponding to the A-phase winding is:

Where Lσ is the leakage inductance of phase A, τ is the pole distance, l is the lamination length, and the above formula can be rearranged to obtain:

Further sorting can be obtained:

So the self-induction of phase A is:

Right now:

Another way to express it:

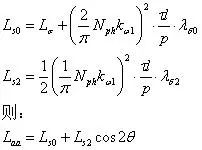
It can be seen that the self-inductance of the A-phase winding is not a fixed value, but changes with the transformation of the rotor. Similarly, the self-inductance of the other two phases can be obtained as:

Lbb=Ls0+Ls2cos2(θ-2π/3)

Lcc=Ls0+Ls2cos2(θ+2π/3)

Calculate mutual inductance between phases

Since the B-phase winding is 120° out of phase with the A-phase winding, it is basically the same as the self-inductance method. We only need to change the integration interval from [-π/2 π/2] to [-π/2-2π/3 π/2-2π/3] to calculate the magnetic flux induced in the B-phase winding by the magnetic field generated by the A-phase winding current. Specifically:

Where Mσ is the mutual leakage inductance, the mutual inductance of A and B can be obtained as:

Similarly, the mutual inductance of the other two phases can be obtained as:

The self-inductance and mutual inductance of a DC motor are shown in the figure below:

How to calculate dq axis inductance?

Generally, DC motors are expressed in dq axis inductance, so the question is: how to calculate or measure dq axis inductance? What is the relationship between dq axis inductance and phase inductance and mutual inductance? What is the relationship between dq inductance and coordinate transformation?

How to determine the coordinate transformation matrix?

The purpose of calculating inductance is to calculate magnetic flux, and then to calculate certain properties of the magnetic field. Through a series of formulas, the self-inductance and mutual inductance of the three-phase winding are finally calculated.

Then the magnetic linkage can be calculated:

The inductance matrix is ​​quite complex:

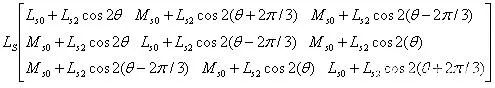
Moreover, this inductance matrix also changes with the change of the DC motor rotor. We can find a similar matrix. This similar matrix is ​​relatively simple in form, with only numbers on the diagonal, and this similar matrix can characterize the key features of the original matrix. The essence of matrix diagonalization is to find the orthogonal basis of the matrix space and the projection coefficients on the "basis". So can the inductance matrix be diagonalized?

You can follow the steps of matrix diagonalization:

Del|Ls-λI|=0

Three eigenvalues ​​can be obtained, namely:

The eigenvector corresponding to the eigenvalue λ1 is:

The eigenvector corresponding to the eigenvalue λ2 is:

The eigenvector corresponding to the eigenvalue λ3 is:

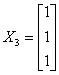
Then the three eigenvectors can form the following characteristic matrix:

This characteristic matrix is ​​the product of Clarke transform and Park transform. The inverse matrix of this characteristic matrix is:

Then the eigenvalues ​​of the inductance matrix can be calculated using the characteristic matrix and its inverse matrix, that is,

λ1 is generally called Ld;

λ2 is Lq; λ3 is L0, that is:

The inductance of the dq axis is the eigenvalue of the three-phase winding inductance matrix. The dq inductance is a constant, and the variable factors such as cos2θ disappear. That is to say, through diagonalization (coordinate transformation), the original complex inductance matrix is ​​diagonalized and constantized, and the stator flux equation is decoupled! At the same time: the dq axis inductance is independent of the transformation matrix and is an inherent property of the inductance matrix.

Constant power conversion

When transforming coordinates, some transformation matrices have a coefficient of 2/3 in front of them, while others have