LeCroy Oscilloscope Basic Application Series II: The Past and Present of FFT

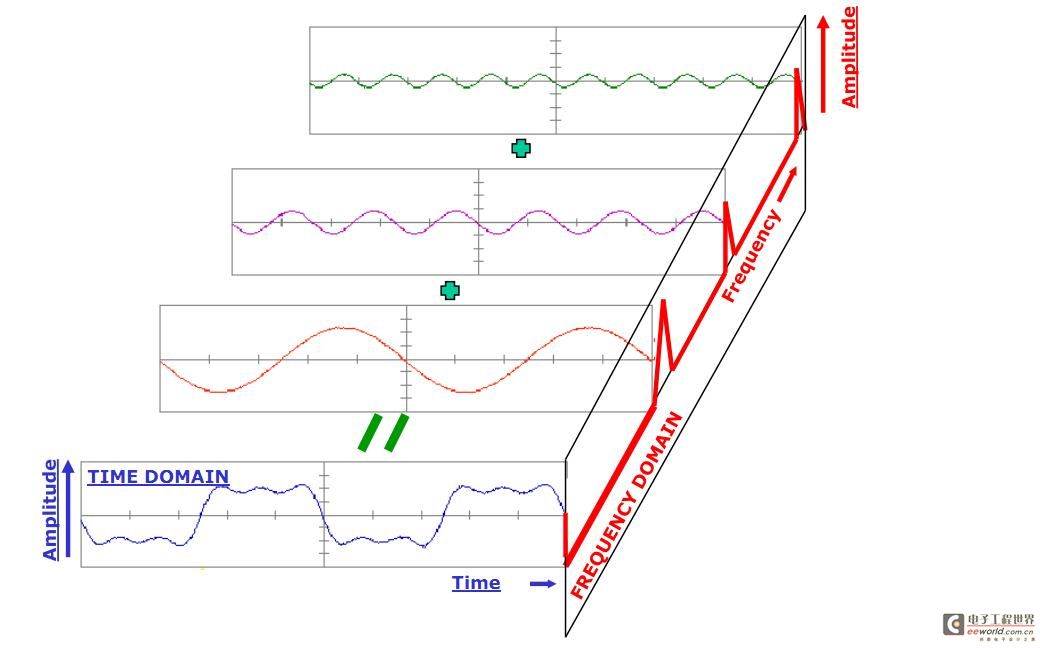
Therefore, after being decomposed by Fourier transform, the time domain signal at the front becomes a superposition of different sinusoidal signals. We then analyze the frequencies of these sinusoidal waves and transform a signal into the frequency domain. It is difficult to see the characteristics of some signals in the time domain, but if they are transformed into the frequency domain, it is easy to see the characteristics. This is why many signal analyses use FFT transforms. In addition, FFT can extract the spectrum of a signal, which is also often used in spectrum analysis.

Fourier transform provides us with the tool to look at problems from a different angle. If we look at problems from a different angle, the problems may be easily solved!

2. How is the transformation carried out?

First of all, according to the type of input signal being transformed, Fourier transform can be divided into 4 types:
1. Non-periodic continuous signal Fourier transform (Fourier Transform)
2. Periodic continuous signal Fourier series (Fourier Series)
3. Non-periodic discrete signal discrete time Fourier transform (Discrete Time Fourier Transform)
4. Periodic discrete signal discrete Fourier transform (Discrete Fourier Transform)

Below are four examples of original signals:
 

Here we are going to discuss discrete signals, and we will not discuss continuous signals, because computers can only process discrete numerical signals, and our ultimate goal is to use computers to process signals. Therefore, only discrete Fourier transform (DFT) can be used for the transformation of discrete signals, and only discrete and finite length data can be processed by computers. Other types of transformations can only be used in mathematical calculations. In front of computers, we can only use the DFT method, and the FFT we are going to discuss is just a fast algorithm of DFT.

The DFT calculation process is as follows:

 
Among them,
X(k)—frequency domain value
X(n)—time domain sampling point
n—sequence index of time domain sampling point
k—index of frequency domain value
N—number of sampling points to be converted

It can be seen that the input value of DFT performed on a computer or oscilloscope is the sampled value collected by the digital oscilloscope after passing through the ADC, that is, the signal value in the time domain. The number of input sampling points determines the calculation scale of the conversion. The transformed spectrum output contains the same number of sampling points, but half of the values ​​are redundant and usually not displayed in the spectrum, so the truly useful information is N/2+1 points.

The FFT process greatly simplifies the process of performing DFT in a computer. Simply put, if the original complexity of calculating DFT is N2 operations (N represents the number of input sampling points), the computational complexity of FFT is Nlg10 (N). Therefore, to calculate a DFT of 1,000 sampling points, the FFT algorithm only needs to be calculated 3,000 times, while the conventional DFT algorithm needs to be calculated 1,000,000 times!

We take a 4-point DFT transform as an example to briefly explain how FFT implements a fast algorithm:

 
Calculated:
 

The red part is the component that must be calculated in FFT, while the other blue parts do not need to be calculated directly and can be directly derived from the red component, for example:
x(1)e-j0 = -1*x(1)e-jπ
x(2)e-j0 = x(2)e-j2π
… …
In this way, the calculated red component only needs the computer to save the result for later calculation, thus greatly reducing the amount of DFT calculation.

3. What is the corresponding relationship between the signals before and after the transformation?

Let's take an actual signal as an example:

The digital signal sampled by the oscilloscope can be transformed by FFT. After N sampling points are processed by FFT, the FFT results of N points can be obtained. In order to facilitate FFT calculation, N is usually an integer power of 2.

Assume that the sampling frequency is Fs, the signal frequency is F, and the number of sampling points is N. Then the result after FFT is a complex number with N points. Each point corresponds to a frequency point. The modulus of this point is the amplitude characteristic at this frequency value. What is the specific relationship with the amplitude of the original signal? Assuming that the peak value of the original signal is A, the modulus of each point of the FFT result (except the DC component of the first point) is N/2 times A. The first point is the DC component, and its modulus is N times the DC component. The phase of each point is the phase of the signal at that frequency. The first point represents the DC component (i.e. 0Hz), and the next point after the last point N (in fact, this point does not exist, it is the assumed N+1th point here, which can also be regarded as dividing the first point into two halves and moving the other half to the end) represents the sampling frequency Fs, which is evenly divided into N equal parts by N-1 points, and the frequency of each point increases successively. For example, the frequency represented by a certain point n is: Fn=(n-1)*Fs/N. From the above formula, we can see that the frequency that Fn can distinguish is Fs/N. If the sampling frequency Fs is 1024Hz and the number of sampling points is 1024 points, 1Hz can be distinguished. The sampling rate of 1024Hz samples 1024 points, which is exactly 1 second. That is to say, if the signal of 1 second is sampled and FFT is performed, the result can be analyzed accurately to 1Hz. If the signal of 2 seconds is sampled and FFT is performed, the result can be analyzed accurately to 0.5Hz. If you want to improve the frequency resolution, you must increase the number of sampling points, that is, the sampling time. The frequency resolution and sampling time are inversely proportional.

The following picture can more clearly show this correspondence:

The width of the spectrum after the transformation (Frequency Span) also has a certain correspondence with the original signal. According to the Nyquist sampling theorem, the maximum width of the spectrum after FFT (Frequency Span) can only be 1/2 of the original signal sampling rate. If the original signal sampling rate is 4GS/s, then the bandwidth after FFT can only be 2GHz at most. The reciprocal of the sampling period (Sample Period) of the time domain signal, that is, the sampling rate (Sample Rate) multiplied by a fixed coefficient is the width of the spectrum after the transformation, that is, Frequency Span = K* (1/ΔT), where ΔT is the sampling period, and the K value depends on whether we downsample (decimate) the original signal before performing FFT, because this can reduce the amount of FFT calculations. As shown in the figure below: [page]
 

 

It can be seen that higher spectrum resolution requires longer sampling time, and wider spectrum distribution requires higher sampling rate for the original signal. Of course, we hope that the spectrum is wider and the resolution is more accurate, so the long storage of the oscilloscope is necessary! It can provide you with the ability to collect signals for a longer time at a high sampling rate! It is worth emphasizing that LeCroy oscilloscopes can support the calculation of 128Mpts FFT, while other brands only have 3.2Mpts.

4. What are the methods and issues to pay attention to when performing FFT using test tools (oscilloscope or other software platforms)?

Let's first look at a simple example---
Problem: We are sampling a continuous, periodic signal on an oscilloscope. We hope to perform FFT calculations on the oscilloscope and observe a spectrum with a center frequency of 2.48 GHz, a bandwidth of 5 MHz, and a spectrum resolution of 10 kHz. How should we set up the oscilloscope to acquire the signal?

First, according to the spectrum resolution (Bandwidth Resolution) of 10KHz, it can be inferred that the minimum time length required to collect the signal is 1/10KHz=100us, so the oscilloscope time base should be set to at least 10us/Div; in order to ensure the signal energy accuracy of the spectrum diagram at each frequency point after FFT, the time domain signal amplitude needs to occupy more than 90% of the entire grid during measurement; the sampling rate setting should at least meet the Nyquist sampling rate, that is, at least set the sampling rate >5GS/s to be able to see the frequency spectrum line with a center frequency of 2.48GHz; select the appropriate window function (Von Hann window) and spectrum display mode (power spectrum); use the Zoom tool to move the spectrum to Center 2.48GHz, Scale 500KHz/Div position, and the Zoom setting method is shown in the figure below:

There are several different output types for FFT calculations in LeCroy oscilloscopes:
Linear Magnitude (Volts),
Phase (Degrees),
Power Spectrum (dBm),
Power Spectral Density (dBm).
These output types are all converted from the results of FFT calculations. We know that the results of FFT calculations contain real and imaginary components, and their units are all Volts. The
specific conversion method is as follows:
Linear Magnitude (Volts) =

Phase(Degrees)=

Power Spectrum(dBm)=

Power Spectral Density(dBm)=

 , where is the spectral resolution and ENBW is the effective noise bandwidth associated with the selected weighting function (window).

Spectrum diagrams of several typical periodic functions:

Spectrum leakage:

The so-called spectrum leakage is the mutual interference between the spectrum lines in the signal spectrum, which causes the measurement results to deviate from the actual value, and at the same time, some false spectra with smaller amplitudes appear at other frequency points on both sides of the real spectrum line. The main reason for spectrum leakage is that the sampling frequency and the original signal frequency are not synchronized, causing the phase of the periodic sampling signal to be discontinuous at the beginning and end. Simply put, because the computer's FFT computing power is limited and can only process FFTs with a limited number of points, when intercepting periodic signals in the time domain, it is not possible to intercept integer multiples of the period. It is impossible to take infinitely large samples when analyzing signals. As long as there is truncation asynchrony, there will be leakage. As shown in the figure below:

 
In the figure, the starting phase and the ending phase of the measured signal are the same, indicating that an integer multiple of the period of the signal is collected within the acquisition time, so the spectrum obtained after the FFT operation will not be leaked.

The signal frequency in the above figure is 2.1MHz. No signal with an integer multiple period is intercepted during the acquisition time. After the FFT operation, the spectrum line leakage phenomenon is serious. It can be seen that the spectrum line with lower energy is easily submerged by the leakage of the adjacent spectrum line with higher energy. [page]

Therefore, in addition to synchronizing the acquisition rate with the signal frequency as much as possible, a method to avoid spectrum leakage can also be to use an appropriate window function.

Another method is to collect the signal for a long enough time to basically cover the entire time span of the effective signal. This method is often used in transient capture, such as impact testing. If the capture time is long enough, the captured signal can always include the moment when the vibration decays to zero. In this case, no window function is required.

The window function is actually a weighted function. It has a value within the intercepted signal time period and a value of 0 outside the time period:
w(t)=g(t) -T/2 w(t)=0 Others

Windowing is a dot product in the time domain, so it is a convolution in the frequency domain. Convolution can be seen as a smoothing process. This smoothing process can be seen as a set of filters with a specific function shape, so the energy at a certain frequency point in the original signal will be combined with the shape of the filter to reduce leakage. Based on this principle, people usually add windows directly in the time domain.
Most signal analyzers generally use rectangular windows, Hanning, flattop and some other window functions.

Different window functions have different effects on the spectrum lines. The basic shapes can be seen in the figure below:

It can be seen that the main lobe width and side lobe attenuation speed of different window functions are different, so the appropriate window function should be used to process the spectrum of different signals.

Rectangular Window: Adding a rectangular window is equivalent to not adding a window, because rectangular interception is used when intercepting the time domain signal. Therefore, the rectangular window is suitable for signals with transient changes. As long as the acquisition time is long enough, the signal width can basically cover the entire effective transient part.

Hanning Window (Von Hann): If the test signal has multiple frequency components, the spectrum is very complex, and the purpose of the test is more focused on the frequency point rather than the energy. In this case, you need to choose a window function with a narrow main lobe, and the Hanning window is a good choice.

Flattop window: If the purpose of the test is to focus more on the energy value of a certain periodic signal frequency point, for example, if you are more concerned about its EUpeak, EUpeak-peak, and EUrms, then the accuracy of its amplitude is more important. You can choose a window with a slightly wider main lobe. The flattop window is often used in such cases.

5. Comparison of FFT calculation methods between LeCroy oscilloscope and Tektronix oscilloscope

You may have discovered this problem: when performing FFT calculations on an oscilloscope, the calculation results using a LeCroy oscilloscope and a Tek oscilloscope seem to be very different. The reason for this difference may be that the effective calculation sampling points of the two are different. Another important reason is that the reference values ​​used for FFT calculations by LeCroy and Tek are different. LeCroy uses dBm as the unit (the reference value is 1mW of power), while Tek uses dB as the unit (the reference value is 1V rms of voltage). Different reference values ​​will of course produce different calculation results!

    dB (Deci-bel) is a pure counting unit, originally intended to indicate the ratio of two quantities, without units. In engineering applications, we often see seemingly different definitions (just different in appearance). For power, dB = 10*lg(A/B). For voltage or current, dB = 20*lg(A/B). Here A and B represent the power value or current or voltage value involved in the comparison. The meaning of dB is actually very simple, which is to express a very large (followed by a long string of 0s) or very small (preceded by a long string of 0s) number in a relatively concise manner.

dBm is a value that measures the absolute value of power, and the calculation formula is: 10lg (power value/1mw).

In addition, there are dBV, dBuV, dBW, etc., which are just different reference value choices.

Here is a tool website that can convert between different comparison values:
http://www.giangrandi.ch/electronics/anttool/decibel.html

The following is an actual measurement example, using the same signal to perform FFT calculations using LeCroy and Tek oscilloscopes respectively.

Test results using LeCroy WaveRunner 64Xi
    
    Test results using Tek DPO4104

The signal amplitude used is 6.55 mV rms and the signal frequency is 25 MHz

LeCroy uses the following calculation method:
dBm = 10 Log10 (((vrms^2)/50)/0.001) = 10Log10 ((4.29E-5/50)/0.001) = 10Log10(8.5E-7/0.001) = 10Log10 (8.5e-4) = 10 (-3.066) = -30.66dBm

The calculation method used by Tek is as follows:
dB = 20Lg (6.61E-3) = 10(-4.3596) = -43.59

The conversion relationship is as follows:

It is not just the difference in FFT calculation methods. Let's take LeCroy's WaveMaster 8Zi-A and Tek's DPO70000 series as examples. On the WaveMaster, you can perform FFT operations on up to 128M sampling points, while on the DPO70000, you can only perform FFT operations on 3.2M points. Therefore, this difference is essential!