Application of image enhancement and restoration technology based on Matlab in SEM images

According to relevant literature at home and abroad, research and development of image processing tools and improvement of image quality are hot topics in today's research. Image enhancement and restoration is a basic image processing technology. It highlights certain information in an image or strengthens certain features of interest according to specific needs, makes the originally unclear picture clear, improves the image quality and enriches the amount of information, improves the visual effect of the image and the clarity of the image components, and strengthens the image interpretation and recognition effect. The purpose of image enhancement and restoration is to process the image to obtain a visually better and easier to distinguish image.

1 Image processing methods

1.1 Histogram Equalization

Histogram equalization (HE) uses the statistical data of the histogram to modify the histogram. It can effectively process the histogram distribution of the original image, so that each gray level has a uniform probability distribution. By adjusting the dynamic range of the gray value of the image, the contrast of the entire image is automatically increased, so that the image has a larger contrast and most of the details are clear. The traditional histogram theory is as follows:

The input histogram is represented by H(p); the input grayscale range is [p0, pk], and the purpose is to find a monotonic pixel brightness transformation q=T(p) so that the output histogram G(q) is uniform in the entire output brightness range [p0, pk]. The histogram can be regarded as a discrete probability density function, and the monotonicity of the transformation T means that the following formula holds:

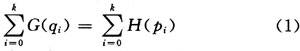
The sum in formula (1) can be understood as the accumulation of discrete probability density functions. Assuming that the image has M rows and N columns of pixels, the equalized histogram G(q) corresponds to the equalized discrete probability density function f, and the value of the function is a constant:

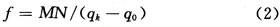
The value of formula (2) is substituted for the left side of formula (1). For the idealized continuous probability density, an accurate equalized histogram can be obtained. At this time, formula (1) changes to:

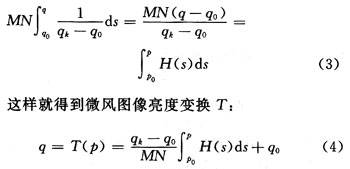
The integral in equation (4) is called the cumulative histogram, which is approximated by summation in digital images, so the resulting histograms are not ideally equivalent. In the discrete case, the approximation of the continuous pixel brightness transformation of equation (4) is:

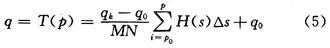
1.2 Frequency domain low-pass filtering

For two-dimensional signals such as images, the spatial domain can be converted to the frequency domain through Fourier transform, and image enhancement operations can be performed in the frequency domain. When analyzing the frequency characteristics of image signals, for an image, the DC component represents the average grayscale of the image; the large background area and the slowly changing part represent the low-frequency components of the image, while its edges, details, jumping parts and granular noise all represent the high-frequency components of the image. Therefore, the process of using a filter function to attenuate high-frequency information on an image in the frequency domain and allow low-frequency information to flow unimpeded is called low-pass filtering. Filtering can remove high-frequency components, eliminate noise, and enhance the smooth image denoising.

The filtering process of the image in the frequency domain is as follows:

(1) Perform Fourier transform on the original input image to obtain the spectrum function F(u, v);

(2) Using the transfer function H(u, v) to process the image spectrum function F(u, v) to obtain the output G(u, v);

(3) G(u, v) is then transformed through inverse Fourier transform to obtain the desired image.

1.3 Adaptive Wiener Filtering

Adaptive Wiener filtering image restoration attempts to use some prior knowledge of the degradation phenomenon (i.e., the degradation model) to reconstruct and restore the degraded image so that the restored image is as close to the source image as possible. The purpose of image restoration is to restore the original appearance of the degraded image as much as possible. To achieve image restoration, it is necessary to understand the cause of degradation, establish a corresponding mathematical model, and restore the image along the inverse process of image quality degradation. Image restoration technology can be divided into unconstrained restoration methods, constrained restoration methods, nonlinear restoration methods, and other methods for image degradation. Here, the adaptive Wiener filter in the constrained image restoration technology is used. The algorithm uses the Wiener2 function for two-dimensional adaptive denoising filtering; this function can perform low-pass filtering on a grayscale image contaminated by additive noise. Its operation rule is that the Winner2 function estimates the local mean and variance around each pixel in image A:

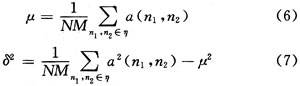
Where N and M represent the N×M local neighborhood around each pixel. The Winener2 function uses these estimates to construct a pixel-wise Wiener filter:

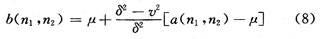
Where: v2 is the noise variance. If the noise variance is not specified, the Winner2 function will use the average of all local estimated variances as its parameter.

2 Application of image enhancement and image restoration technology in SEM images based on Matlab

The algorithm is used to enhance and restore medical biological images. As shown in Figure 1, the original image is blurred, the dynamic range is small, and the entire image presents low contrast. Image 2 processed by histogram equalization significantly enhances the contrast of the entire image, and the epithelial cells are clearly distinguished from the surrounding environment, but the image is not smooth and has noise. Figure 3, which has been processed by low-pass filtering, removes high-frequency components and eliminates noise through filtering, which enhances the smooth image and removes noise, but because it removes frequency components corresponding to certain boundaries, the boundaries of epithelial cells become a little blurred. Figure 4, obtained by adaptive Wiener filtering, has greatly improved the image quality of epithelial cells, highlighting the overall and local characteristics of epithelial cells, and achieving good visual effects and distinguishing features.

3 Conclusion

The original pictures used were taken and saved by the author during the scanning electron microscope work. The cells and the background are not clearly distinguished. No matter how the electron microscope is operated, the clear cell outline desired by the customer cannot be achieved, and the cell outline is clearly distinguished from the surrounding environment. Image enhancement can be understood as appropriate transformation as needed, emphasizing or sharpening certain features of the image, such as edges and contour contrast, highlighting certain useful information, removing or weakening useless information, so as to facilitate display, observation or further analysis and processing. Visual evaluation of image quality is a highly subjective process.

As shown in Figures 1 to 4, the images in the original pictures are blurred, with low contrast, unclear outlines of epithelial cells, and little distinction from the background. After histogram equalization, frequency domain low-pass filtering, and adaptive Wiener filtering, the images are gradually improved. The resulting image (see Figure 4 for the image after adaptive Wiener filtering) has very clear outlines of epithelial cells, moderate contrast and brightness, and can be used well in biomedical work to identify epithelial cells. Digital image processing can well enhance and improve the quality of such images in biomedicine. During the scanning electron microscope operation, because cells (epithelial cells, calcium cells, nerve cells, etc.) are too similar to the surrounding environment, no matter how the electron microscope is operated, it is impossible to obtain an ideal image with clear cell outlines and clear distinction from the background. Digital image processing provides a technical platform for the processing of medical biological images, which is not only of great significance for the analysis and diagnosis of biomedical images, but also of great reference significance for other image processing.