Making Accurate Resistance Measurements - Measurement Parameters Chapter 6

Resistance Measurement Principle

At first glance it might seem strange to have a chapter on resistance measurement. After all, every electrical engineering student learns the simplest Ohm's law for determining resistance in the first week:

V = I × R (Formula 6.1)

Although this formula is very simple, accurately measuring resistance is actually a very challenging parameter to measure. Because the formula is too simple, it ignores the fact that the resistor will generate heat, which in turn affects the resistance value itself. Therefore, the above formula should be rewritten more accurately as:

V = I × R (T) (Formula 6.2)

In the formula, resistance (R) is a function of temperature (T). This phenomenon in which the actual value of the measured resistance changes as the heat generated by the current is usually called the Joule self-heating effect.

Another factor to consider is the resistance of the cable used to make the resistance measurement. When measuring very small resistances, you must use Kelvin measurement techniques. We have introduced the basics of Kelvin measurements in previous chapters, and you can apply these techniques directly to resistance measurements. However, it should be noted that the combination of Joule self-heating and cable resistance makes resistance measurements more challenging. To reduce Joule self-heating, you need to reduce the current flowing into the resistor being measured (reduce the power). However, to distinguish the voltage drop caused by a small current flowing through the cable from the voltage drop through the resistor being measured will require the measurement equipment to have very accurate voltage measurement capabilities. For these reasons, resistance measurements often require voltage measurement resolution of more than 1 mV.

电阻测量要考虑的最后一项因素是电动势(EMF)。EMF 是机械继电器断开或闭合时所产生突发电噪声的技术名称。当SMU 被激活时，在输出路径上有机械继电器(干簧继电器) 的所有SMU 都会产生EMF。 EMF 对所有各种类型测量的测量准确度都有显著影响，尤其是对低阻测量，因为低阻测量要求非常灵敏的电压测量分辨率。

Resistivity

Resistivity is a fundamental property of materials. If a voltage is applied and a current is measured across a homogeneous material with a uniform cross-section, the resistance value can be determined using the formula R = V/I. If the cross-sectional area (width x depth) and length of the sample are known, the resistivity property of the material in question can be calculated from the resistance measurement, as shown in the figure below.

Figure 6.1 — Calculation of resistivity from resistance measurements

Generally, it is necessary to measure the sheet resistivity of all buried layers and metal interconnect layers. Resistivity is usually expressed in "ohms per square", that is, the resistance of a square homogeneous material is always the same regardless of the area.

Figure 6.2 — A square of homogeneous material of the same thickness has the same resistance value regardless of area.

Van der Pauw test structure

When making resistivity measurements, the Kelvin measurement technique must be used because the resistance being measured can be very small (in the order of milliohms). Therefore, the sheet resistance of a given material can be determined very easily by combining the Kelvin measurement technique with a simple geometry. Such a common configuration is called a Van der Pauw structure, named after Van der Pauw, who first proposed this measurement technique in 1958. As shown in the figure below, a Van der Pauw structure is a square sample with electrical contacts at the corners.

Figure 6.3 — Van der Pauw test structure for determining resistivity

In his original paper, Vanderbilt established that the following relationship holds:

Here d is the sample thickness,  is the sheet resistance of the sample, and the resistance measurement is defined as follows.

Figure 6.4 — Calculation of sheet resistance from the Van der Pauw test structure

The resistivity can be easily calculated from the formula and the measurement results.

Take into account Joule self-heating effect

Joule self-heating limits the accuracy of resistance measurements by changing the value of the resistor being measured. But if you choose the maximum resistance change you can tolerate, you also determine the maximum power dissipation you can allow. The equation for the power dissipated in a resistor is:

By rearranging the above equations and solving for voltage, the maximum power dissipation can be converted to the minimum acceptable voltage resolution required to meet the resistance measurement requirements. The formula that describes this relationship is:

Figure 6.5 — Thermal properties of silicon dioxide

This means that if you apply 1W of power to a 1 cm square of this metal structure, the temperature will rise by 0.007°C; but if you apply 1W of power to a 10 µm square of this metal structure, the temperature will rise by 7000°C. Of course, in this case, the metal on top of the SiO2 will evaporate completely before the temperature reaches 7000°C. This example is to show that you cannot arbitrarily add power (=current) to the resistor to compensate for the lack of measurement hardware accuracy. The resistance change of copper or aluminum wire near room temperature is about 0.35%/°C. For the above situation, we can calculate the maximum power dissipated by a 10 mm x 10 mm copper or aluminum metal sheet to produce a 0.1% resistance change.

To achieve 0.1% accuracy in a copper Vanderbilt structure (1 mm thick film) with an equivalent resistance of 10 mΩ per square, we have:

This means that the measuring instrument must be able to resolve voltages as low as 1 mV! Note: The Vanderbilt structure is an extreme example. A 0.1% accuracy on a 1 mm wide, 100 mm long metal line typically requires the measuring instrument to be able to resolve to the order of 10 mV. We know that the maximum allowable voltage is proportional to the square root of (Pmax x R), and the required voltage resolution increases with the square root of the resistance value. Since this is a relatively weak dependence on the resistance value, 10 mV is a good estimate of the required measurement resolution for most resistance measurements.

Eliminate the influence of electromotive force (EMF)

What is Electromotive Force (EMF)?

Electromotive force (EMF) is the name for the transient voltage generated when a reed relay is switched on and off. Conventional reed relay switches used in various sources typically generate thermal EMFs ranging from tens to hundreds of microvolts after switching on or off. The resulting voltage drift can last for several minutes, which is unacceptable for parameter testing that requires precise measurements. The figure below is an example of the thermal EMF generated by a commercial reed relay.

Figure 6.6 - Thermal EMF generated by a typical reed relay

It is important to note that the graph above is not the characteristics of a reed relay used in parametric measurement instruments (for obvious reasons). Agilent has developed a patented reed relay technology called "cold protection". These relays used in parametric measurement equipment minimize EMF effects and thereby improve measurement throughput and accuracy. The performance characteristics of a cold protection relay are shown below.

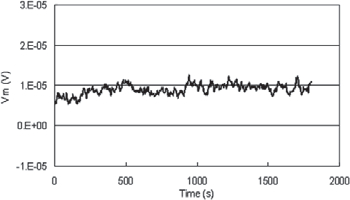
Figure 6.7 - Thermal EMF generated by a Keysight cold protection relay

For simplicity, the output relay switch is not included in the SMU circuit diagram discussed in Chapter 3. However, it is important to understand that all SMUs have switches in their output paths, which also generate electromotive force when they are turned on or off. The following is a revised SMU circuit diagram.

Figure 6.8 - SMU circuit diagram showing output connected to relays

When using the SMU from the instrument's front panel, the software closes and closes the relay as needed, so it is invisible to the user. However, when using the instrument under program control, the user must issue a connect ("CN") command to close the relay, and the relay will remain closed until a command (such as "* RST") is issued to open the relay.

Mitigating EMF Effects

Mitigating the effects of EMF on parametric measurements is relatively simple. It should be noted that thermal EMF is already accounted for in the specifications, so it is not necessary to consider thermal EMF in general measurements. However, when making extremely sensitive measurements, or trying to achieve higher measurement accuracy in parametric measurement equipment, the following principles can minimize or eliminate EMF effects:

1. Make sure the output relays are closed and stabilized to their final values. This means the instrument has warmed up and the SMU output relays remain closed.

2. Complete any measurements as quickly as possible (under 10 seconds). This will keep the measurement drift to within a few millivolts.

A resistance measurement technique that can eliminate both the effects of the EMF and any offset voltage of the measurement device is to make two resistance measurements using the Kelvin measurement technique, reversing the polarity of the drive current in the second measurement. If you apply Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL) to this circuit, you can see that by averaging the two measurements, the offset voltage and EMF will cancel out, giving you the true resistance value.

Figure 6.9 – By measuring the resistance twice and averaging the results, the effects of EMF and voltage offset are eliminated.

To summarize the key points of the above techniques:

1. Make sure the applied current is low enough to eliminate any Joule self-heating effects.

2. Make two resistance measurements by reversing the polarity of the applied current and then average the two measurements.

3. If possible, use a voltmeter instead of an SMU to measure voltage because a voltmeter generally has higher measurement accuracy.