Fixed-point DSP implementation of fast wavelet transform

Fixed-point DSP implementation of fast wavelet transform

Wavelet transform has good time-frequency locality and is an important method for analyzing singular signals. Fixed-point DSP is widely used in engineering, with the characteristics of low cost and high performance. Using DSP to implement wavelet transform can meet the real-time requirements of engineering. This paper briefly introduces the theory and algorithm of wavelet transform, and explains the implementation of the algorithm with TI's 16-bit fixed-point DSP.
Keywords: fast algorithm, wavelet transform, DSP

1 Introduction
Wavelet transform is a mathematical theory and method developed in recent years. As an emerging theory, wavelet analysis is an important achievement in the history of mathematical development and has a profound impact on engineering applications. It is widely used in speech signal processing, image signal processing, signal detection, speech and image coding, multi-scale edge extraction and reconstruction, etc. In recent years, wavelet analysis has also been used in power systems for fault detection and fault location, and effective results have been achieved.

Computers can only process digital signals, so in actual signal processing, discrete wavelet transform (DWT) is often used. Due to the complexity of the wavelet transform algorithm, although the computing speed of today's processor chips has been greatly improved, it still cannot meet the requirements in terms of real-time performance. In order to simplify the calculation process, people have developed some fast algorithms, such as the Mallat tower algorithm, and algorithms that use chirped Z transform (CZT) and Mellin transform (Mellia Transform) for fast calculation. Among them, the Mallat tower algorithm is particularly widely used in practice.

In the field of digital signal processing, dedicated digital signal processor chips (DSP) are usually used to complete specific computing requirements. TI, an American company, is the world's largest DSP supplier. Its TMS320C2xx series of 16-bit fixed-point DSP chips have the characteristics of high performance and low price, and have a wide range of applications. In this paper, this series of DSP chips are used to implement a fast algorithm for wavelet transform.

This paper implements the fast wavelet transform algorithm with DSP, which can not only use wavelet transform to achieve application requirements, but also reduce costs and enhance market competitiveness. Especially today, with the continuous development of power systems and users' higher and higher requirements for power quality, the number of sampling points for power system operation monitoring and protection is increasing. This method can solve the problem of large amount of calculation and high calculation accuracy.

2 Wavelet transform and algorithm
2.1 Wavelet transform
The exact definition of wavelet function is:
let ψ(t) be a square integrable function, if its Fourier transform ψ(ω) satisfies the condition

then ψ(t) is called a basic wavelet or wavelet mother function. After scaling and translating it, we get the wavelet basis function

The so-called wavelet transform is to expand the signal under the above wavelet basis. Of course, this transform must have an inverse transform, otherwise, the original signal cannot be restored and the transform is meaningless.

2.2 Multi-resolution analysis
Multi-resolution analysis plays a very important role in the theory of orthogonal wavelet transform. Before the emergence of multi-resolution analysis theory, people had to rely on skills to construct orthogonal wavelet basis functions, which was difficult. Since the emergence of multi-resolution analysis theory, this work has become much easier. Of course, it still requires some experience to find a suitable basis function. Once the suitable filter coefficients are found, the fast wavelet algorithm given by Mallat can be used to calculate the wavelet transform.

In layman's terms, multi-resolution analysis is to decompose the function f(t) in space V0 into a detail part W1 (wavelet space) and a large-scale approximation part V1 (scale space), and then further decompose the large-scale approximation part V1. By repeating this process, you can get the approximation part and detail part at any scale (or resolution).

2.3 Filter coefficients
According to the multi-resolution analysis theory, if φ(t) and ψ(t) are standard orthogonal basis functions of scale space V0 and wavelet space W0 respectively, then there is a relationship between the two scale space basis functions between any adjacent scales j and j-1 Among them,

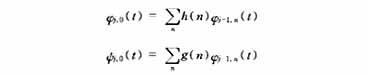
h(n) and g(n) are filter coefficients, which are determined by the scale function φ(t) and the wavelet coefficient ψ(t).

[page]
2.4 Mallat Tower Algorithm
Once we have a set of wavelet basis functions, the remaining thing is to calculate the decomposition, that is, to express the signal with wavelet basis functions, so the key issue is to find the coefficients in the expression. According to multi-resolution analysis, the signal f(t)□Vj-1 is decomposed once (that is, projected to Vj and Wj space respectively). At this time, cj,k and dj,k are the expansion coefficients on the j scale. After a relatively simple derivation, we can get

where cj,k and dj,k are called the residual coefficients and wavelet coefficients of the j scale space respectively. The above formula shows that they can be obtained by weighted summation of the residual coefficients cj-1,k of the j-1 scale space through the filter coefficients. In practice, the lengths of filters h and g are finite or approximately finite, so the decomposition operation is very simple. Further decomposing cj,k, we can get the residual coefficients Cj+1,k and wavelet coefficients dj+1,k of the Vj+1 and Wj+1 spaces respectively,

thereby obtaining the decomposition on any scale space. The decomposition process is shown in the figure

In the above algorithm, there must be an initial input sequence Cj-1, k for the decomposition to proceed smoothly, which is a problem. In most applications, for simplicity, the sampling sequence of the input signal is often used to approximate C0, k. Several other methods for determining C0, k are also given in some literature.

3 Implementation of the algorithm on DSP
Assume the input signal x(t), sampling frequency N(=2n), and obtain the sampling sequence x(k), k=0, ..., N-1, as the initial input sequence C0, k. Filter coefficients h(m), g(m), m=0, ..., L-1. For ease of application, equations (1) and (2) can be changed to

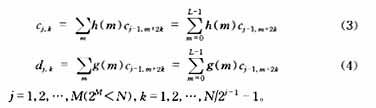
Starting from the first scale j=1, calculate the weighted sum of the filter coefficients and the remaining coefficients, and obtain cj, k and dj, k respectively, and their lengths are both N/2. Calculate the scale values ​​of j=2, 3, ... in turn, and the lengths of cj, k and dj, k will also become N/4, N/8, .... It should be noted that when the filter coefficient sequence is multiplied by the input signal sequence, each coefficient is multiplied in turn and then accumulated to obtain the cj, k or dj, k value. After calculating one, the filter coefficient sequence should be moved back two positions and then multiplied with the input signal. Finally, when there are only two values ​​left, continue from the first position to form a circular form and get the last cj,k and dj,k. Take j=1 as an example to illustrate this point.

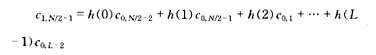
Similarly, d1,N/2-1 can be obtained. ?
In the TMS320C2xx series fixed-point DSP, there is no addressing method to directly implement the above algorithm, which can be implemented using loop instructions. Among them, the two important instructions to be used are MAC (multiply-accumulate instruction) and RPT (repeat instruction). The MAC instruction is one of the most distinctive instructions in DSP instructions. When the RPT pipeline is started, the multiplication and addition operation can be implemented in a single instruction cycle through the MAC instruction. The key to the algorithm is a convolution calculation, and its process can be implemented with the following statements. Assume that the program memory address 0xFF00h starts, and the wavelet filter coefficients h(k), k=0, 1, 2, ..., L-1 are stored, and the wavelet filter coefficients g(k), k=0, 1, 2, ..., L-1 are stored starting from 0xFF80h. The data register address 0x1000h (indicated by cc) starts to store the input signal. The program for calculating c1, k is as follows
RPTL-1
MAC0FF00h, cc+2*k.
The following briefly introduces the calculation process on a single scale. It is still assumed that the input signal is a sample value of N points and the length of the wavelet filter is L.
Due to the above circular form of the loop algorithm, it is very inconvenient to directly calculate all values, so the whole process is divided into two parts. In the first part, save c0, k (k=N-2, N-1, 0, 1, 2, ..., L-3) to a continuous storage space, and then calculate the value of d1, k when k＜N／2-L, and save it to the temporary storage space datad (requires N units). The second part calculates the value of d1, k when k=N／2-L, ..., N／2-1 and saves it in datad (starting from the N／2-L unit). Calculate the values ​​of c1,0, c1,1,…, in the same way as before, and overwrite the original c0,0, c0,1,…, when saving. If it is convenient to reconstruct the coefficients, the first N/2 units in datad can be moved to the original c0,k (k=N/2,…,N-1) position. In this way, the decomposition coefficients can be obtained.

4 Conclusion
Wavelet analysis has good time-frequency locality and is one of the most popular analysis methods today. Using fixed-point DSP for wavelet transform meets the real-time requirements, has good accuracy and low cost, and is an ideal choice in the field of industrial control.