DSP implementation of FIR digital filters of different orders

　　The structure of the FIR filter is mainly non-recursive and has no feedback from the output to the input. And the FIR filter can easily obtain strict linear phase characteristics and avoid phase distortion of the processed signal. The linear phase is reflected in the time domain only as the time delay of h(n). This feature is very important in waveform transmission systems such as image signal processing and data transmission. In addition, it will not cause blocking and can prevent strong signals from overwhelming weak signals, so it is particularly suitable for situations where there is a huge difference in signal strength. Its main disadvantage is that its better performance comes at the expense of a higher order. Therefore, while ensuring the same performance, striving to reduce its order is one of the important factors in the design of FIR digital filters.

　　The following introduces the general mode of applying Matlab and DSP chips to implement FIR filters.

1 Design method of FIR filter

　　It is usually simple to design FIR filters using the window function method, but the design of these filters is not yet optimal. First of all, the fluctuations of the passband and stopband are basically equal. Although δ2<δ1 is generally required, these parameters cannot be controlled separately in the window function method. In addition, for most window functions, the fluctuations within the passband or stopband are not uniform and usually decrease when leaving the transition band. If the fluctuations are allowed to be evenly distributed throughout the passband, smaller peak fluctuations will result.

　　The optimal design is to use all sampled values ​​as variables and to obtain the optimal result through computer iterative calculations under a certain optimization criterion. The optimization criterion can use the mean square error criterion. However, practice has proven that the equal ripple approximation method applying the maximum error minimization criterion is a more practical method. When applying this method, the order, the edges of the passband and stopband, and the weighting function of the error can be freely selected, which is very flexible. The error of the designed filter is evenly distributed over the entire frequency range, so it can approach the proposed index requirements at the lowest order.

　　Assume that the amplitude-frequency characteristic of the filter to be designed is HdA(ω), and the amplitude-frequency characteristic of the actually obtained filter is HA(ω). The purpose is to make HA(ω) best approach HdA(ω). The best consistent approximation of equal ripples is to derive a set of conditions based on the design requirements to minimize the absolute value of the approximation error in the entire approximation frequency region. A weighting function W(ω) is defined. W(ω) can be obtained in different frequency bands. Different values ​​can be used to freely determine the weight of the error in each frequency band. When optimizing the design, W(ω) is a known function, so the weighted error function E(ω) can be defined as:

　　　

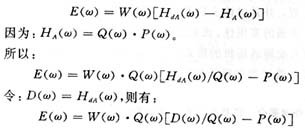
　　Since Q(ω) is a known trigonometric function, the above formula is valid everywhere except at the point ω=0,π. make:

　　?

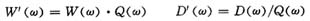
　　Then the following mathematical model can be obtained:

　　?

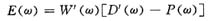
　　Based on this, the design problem of the FIR filter can be summarized as the following weighted Chebyshev approximation problem: find a set of coefficients a(n) of P(ω) (or make the maximum absolute value of E(ω) throughout reaches the minimum in the frequency band. That is:

　　?

　　Among them: B represents the entire meaningful frequency band.

　　The basis for solving Chebyshev's approaching problem is the interleaving theorem (which will not be introduced here).

2 Use Matlab to design FIR digital filter

　　The Matlab signal processing toolbox uses the Remez algorithm to realize the optimal consistent approximation design of the linear phase FIR filter with equal ripples. Compared with other design methods, its advantages are: when the design indicators are the same, the filter order is the lowest; when the order is the same, the passband is the flattest and the stopband is the smallest attenuation; both the passband and the stopband are in the form of equal ripples , suitable for designing fragment constant filters. Its calling format is as follows:

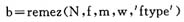
　　The remezord function is used to estimate the lowest order N of the equal-ripple best consistent approximation design of the FIR digital filter, so that the filter has the lowest cost while meeting the specifications. The basic calling format is as follows:

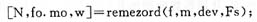
　　Its return parameters are used by the remez function. Compile program (omitted) filter simulation program of FIR digital filter:

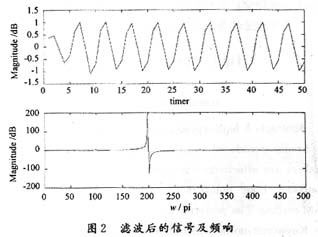
　　Suppose there is a sinusoidal superposition signal: x=sin(2*pi*100*t)+sin(2*pi*200*t)+sin(2*pi*3 00*t); after passing through the band-pass filter , filter out signals with frequencies of 100 Hz and 300 Hz, as shown in Figure 1. The results are shown in Figure 2.

3 Use DSP linear buffer and dual-operand addressing method with displacement to implement FIR digital filters of different orders

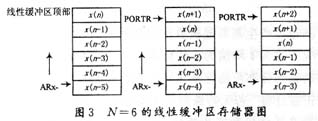
　　The core device implemented uses the DSP chip TMS320C5402 produced by Texas Instruments Company of the United States. For an N-stage FIR filter, a buffer of N units called a sliding window is opened in the data memory to store the latest N input samples. Starting with the oldest sample, shift the sample downward after each sample is read. After reading the last sample, enter the latest sample to the top of the buffer (see Figure 3). The main program of the FIR filter (see Figure 4 for the program flow chart) includes three subroutines: Variableinc, Bfunction.asm, and Filter_coeffinc. The main function of the Variableinc program is to define the TMS320 registers as global symbols, so that the registers (symbols) can be directly referenced. The main function of the Bf unction.asm program is to initialize FEC and initialize C54. The Filter_coeff.inc program provides the coefficients of the filter, whose coefficients are expressed in Q15 format.

　　　　　　　　　　?

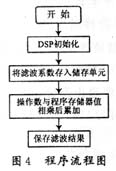
4 Conclusion

　　Practice has proved that the filter has high accuracy, good stability, easy transplantation and strong practicality and flexibility. Mat lab can easily design FIR digital filters and modify the coefficients easily. Due to the good portability of DSP, filter coefficients obtained from different methods can be written into the filter_coeff.inc subroutine to obtain different filtering effects.

references

1] Ding Yumei, Gao Xiquan. Digital signal processing [M]. Xi'an : Xi'an University of Electronic Science and Technology Press, 2002 2] Wu Xiangqi. Signals, systems and signal processing [M]. Beijing : Electronic Industry Press, 1999.
3] Xue Nianxi .Application of Matlab in digital signal processing [M]. Beijing: Tsinghua University Press, 2003. 4] TMS320C54X DSP CPU and Peripherals (Reference Set Volume 1).
5] TMS320C54X DSP Mnemonic Instruction Set (Reference Set Volume 2).