Briefly describe the SVPWM principle of FOC motor control (Part 1)

SVPWM (Space Vector Pulse Width Modulation) is space vector pulse width modulation. The theoretical basis of SVPWM is the average value equivalent principle, that is, in one switching cycle Ts, the basic vector voltage is combined so that its average value is equal to the given voltage vector. By controlling the action time of the basic vector voltage, the synthesized target vector voltage rotates in a circular trajectory in the spatial position, and the actual magnetic flux generated approaches an ideal magnetic flux circle. The model is shown in the figure below. The more sampling points there are, the closer it is to the ideal magnetic flux circle. In theory, when the number of sampling points is infinite, it is the ideal magnetic flux circle.

Left: Basic voltage vector diagram; Right: Schematic diagram of actual magnetic flux circle trajectory

The terminal voltages applied to the three-phase winding coils are all sinusoidal voltages. Let the peak value be Um, and the phase difference between the two phases is 120°, which can be expressed as:

Note: The voltage here is a scalar, but the voltage amplitude changes sinusoidally.

In the two-dimensional plane, the coordinate system formed by the three-phase winding ABC has a 120° difference between the coordinate axes. The three-phase basic voltage is expressed by a vector:

Using Euler's formula

Expand the above formula and calculate its vector sum

The following is the process of expanding the calculation:

The expansion formula of trigonometric functions is used in the calculation process:

Principle summary:

The target voltage is synthesized by three basic voltages that are 120° apart in space. The directions of the three basic voltages remain unchanged, the amplitudes change according to the sine law, and the phases differ by 120°; the amplitude of the synthesized target vector voltage is fixed and unchanged, which is 1.5 times the peak value of the phase voltage, and the direction rotates in space, and the angular velocity of rotation is equal to the angular velocity of the phase voltage amplitude change.

02. SVPWM Implementation Method

2.1 Basic vector voltage:

As shown in the figure below, the three-phase bridge arm of the inverter has a total of 6 switch tubes (Q1, Q2, Q3, Q4, Q5, Q6). For each half bridge, only one switch tube can be turned on at the same time, that is, the control signals G1 and G2 are reversed, G3 and G4 are reversed, and G5 and G6 are reversed. If the upper and lower bridge arms of the same half bridge are turned on at the same time, the power supply Udc will be short-circuited. The outputs of the three half bridges of the inverter are added to the ABC three-phase windings of the motor respectively, and the three-phase windings are 120° apart in space.

Defining the switch function

If S(A)=1, it means Q1 is on and Q2 is off, and the bus voltage Udc is added to the A phase winding;

For example, S(B)=1 means Q3 is turned off and Q4 is turned on, and the B-phase winding is connected to the negative pole of the power supply, that is, GND.

There are 8 combinations of the states of the three switching functions ABC (S(A), S(B), S(C)), which are {(0,0,0),(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,0),(1,1,1),}, corresponding to 8 vector voltages, of which the 2 zero vector voltages are and , and the 6 non-zero vector voltages are , which are adjacent to each other in space with an interval of 60°, dividing the plane into 6 sectors.

Taking the common end point N of the three-phase winding as the reference zero potential, the directions of the basic vector voltages are shown in the figure above. In the three-phase coordinate system, the amplitudes of these six non-zero basic vector voltages are Udc, as shown in the following table.

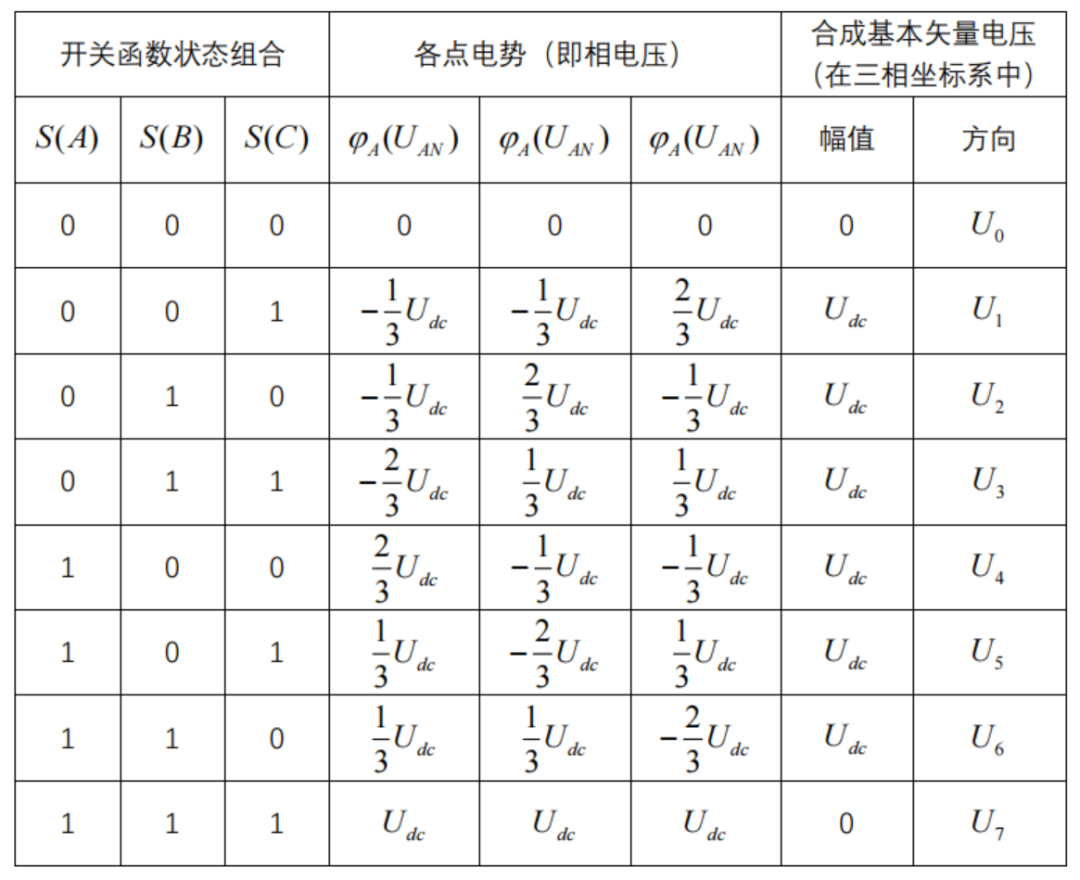
It is easy to imagine that by controlling the state of the switch tube, a vector voltage in any of the six directions can be synthesized; by controlling the PWM duty cycle of the switch tube in this state, the effective value of the amplitude of the vector voltage in this direction can be changed (the duty cycle from 0 to 100% corresponds to the effective value of the vector voltage from 0 to Udc). For example, to synthesize a vector voltage with the same direction as U4 and an amplitude of Udc/2, you only need to control the duty cycle of G1 to 50%, and the duty cycles of G3 and G5 to 0%; for another example, to synthesize a vector voltage with the same direction as U6 and an amplitude of 3Udc/4, you only need to control the duty cycle of G1 and G3 to 75%, and the duty cycle of G5 to 0%.

In the three-phase coordinate system, the amplitudes of the six basic vector voltages are all Udc. Converted to the αβ two-phase coordinate system, the amplitude of the basic vector voltage is 2*Udc/3 (why it is 2/3 times? This question troubled me for a long time before I figured it out. Let me briefly explain it below).

Taking the basic vector voltage U1 as an example, the amplitude of U1 (001) in the abc three-phase coordinate system is Udc, which is synthesized by . After Clarke transformation, the voltage in the αβ two-phase coordinate system is obtained , and the amplitude of the basic vector voltage U1 synthesized in the two-phase coordinate system is , and the direction remains unchanged. Because we judge that the output target vector voltage of the sector and PID calculation is performed in the two-phase coordinate system, the calculation of SVPWM is also performed in the two-phase coordinate system.

The following introduction is all based on the two-phase coordinate system, please note!

After the above steps, we can synthesize 6 basic vector voltages with amplitudes of in 6 directions. Next, we use these 6 basic vector voltages to synthesize a vector voltage with any direction of 0-360° and any amplitude of 0~Umax, which is our final target vector voltage. The value of Umax is calculated below.

It is easy to know that the maximum rotating circular target voltage that can be synthesized through these 6 basic vector voltages has an amplitude equal to the radius of the inscribed circle of the regular hexagon, that is .

Let's review the math: In a plane, two non-collinear non-zero vectors can be used as a basis, and the linear combination of the two bases can synthesize a third vector of any direction and size in the plane. (It doesn't matter if you don't understand, just read on)

It is easy to imagine that any target voltage vector can be synthesized from two adjacent basic vector voltages of the sector where the vector is located. For example, any vector voltage Us of sector I can be synthesized from two adjacent basic vector voltages U4 and U6.

Here Us is the vector sum of Uq and Ud in the coordinate transformation. (PS: In motor control applications, Uq is calculated and output by the q-axis current loop PI controller, and the d-axis current loop also calculates and outputs a Ud, which lags behind Uq by 90°)

Then we return to the coordinate transformation, which is explained in detail in another article [link to another article], so here we will just briefly explain the results.

First, the inverse park transform is used to calculate Uα and Uβ from the expected output Uq and Ud and the current spatial position, that is, the angle θ [in motor control, this refers to the electrical angle, not the angle of the rotation plane (the relationship between the electrical angle, the number of motor pole pairs and the rotation angle will be discussed later)].

After getting Uα and Uβ, the next step is to determine the sector

2.2 Sector determination:

The target vector voltage Uref is the vector sum of the outputs Uq and Ud calculated by the PI controller. Uα and Uβ are obtained through Park inverse transformation. The first step of space vector modulation is to determine the sector where the target space vector voltage is located based on Uα and Uβ.

From the above vector diagram geometric relationship analysis, we can get the list of necessary and sufficient conditions that need to be met in the sector:

It can be seen that the basic variables that determine the sector are:

There are only three linearly independent ones (you can also choose three other linearly independent ones):

Then (A, B, C) has 8 states: 000, 001, ……………, 111

Among them, (A, B, C) = (000) and (111) do not exist, and the other 6 states correspond to 6 sectors. A simple analysis is given below.

When (A,B,C) = 000:

That is, U1<0,U2<0,U3<0,

That is, Uβ<0. By superimposing equation 2 and equation 3, we get -Uβ<0, Uβ>0, which conflicts with equation 1. Therefore, this state does not exist.

When (A, B, C) = 001:

That is, U1<0,U2<0,U3>0,

That is, Uβ<0, so the electrical angle θ satisfies: 180<θ<360;

Under the condition of Uβ<0, the cases of Uα>0 (270360) and Uα<0 (180270) are discussed, and combined with equation 2 and equation 3, namely:

When (A, B, C) = 010:

That is, U1<0, U2>0, U3<0,

That is, Uβ<0, so the electrical angle θ satisfies: 180<θ<360;

Under the condition of Uβ<0, the cases of Uα>0 (270360) and Uα<0 (180270) are discussed, and combined with equation 2 and equation 3, namely:

When (A, B, C) = 011:

That is, U1<0,U2>0,U3>0,

That is, Uβ<0, so the electrical angle θ satisfies: 180<θ<360;

Under the condition of Uβ<0, the cases of Uα>0 (270360) and Uα<0 (180270) are discussed, and combined with equation 2 and equation 3, namely:

When (A, B, C) = 100:

That is, U1>0, U2<0, U3<0,

That is, Uβ>0, so the electrical angle θ satisfies: 0<θ<180;

Under the condition of Uβ>0, the cases of Uα>0 (090) and Uα<0 (90180) are discussed, and combined with equation 2 and equation 3, namely:

When (A, B, C) = 101: