| Overview : |
|
At present, when explaining the fast Fourier transform (FFT), the textbooks on digital signal processing in China all focus on complex FFT, and the real FFT algorithm is only briefly mentioned. The specific implementation programs given in the books are mostly BASIC or FORTRAN programs and most of them cannot be actually run. In view of the fact that FFT operations are currently used in many embedded systems, such as AC sampling systems with DSP as the core, spectrum analysis, correlation analysis, etc., I have studied the real FFT algorithm based on my actual development experience and given a specific C language function, which readers can directly apply to their own systems.
First, the derivation process of the real number FFT algorithm is analyzed, and then a C language program that implements the FFT algorithm is given, which can be directly applied to embedded systems such as microcontrollers or DSPs that require FFT operations.
The FFT algorithm of decimation in time (DIT) usually stores the original data in reverse order and finally outputs the results X(0), X(1), ..., X(k), ... in normal order. Assume that at the beginning, the data is in the array float dataR[128]. We represent the subscript i as (b6b5b4b3b2b1b0)b. The reverse order storage is to store the original element at the i-th position at the (b0b1b2b3b4b5b6)b position. Since the C language has a strong bit operation capability, we can extract b6, b5, b4, b3, b2, b1, b0 respectively and then reassemble them into b0, b1, b2, b3, b4, b5, b6, which are the reverse order positions. The program segment is as follows (assuming 128-point FFT):
You can compare it with the bit reversal program in the textbook and you will find that this algorithm makes full use of the bit operation capabilities of the C language. It is very easy to understand and the bit operation speed is very fast. 2 Derivation of the real number butterfly operation algorithm Let’s first look at the butterfly diagram shown in Figure 1. |
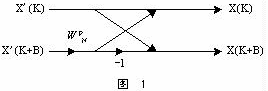
|
|
Butterfly formula:
X(K) = X'(K) + X'(K+B)W PN , X(K+B) = X'(K) - X'(K+B) W PN where W PN = cos(2πP/N) - jsin(2πP/N). Assume X(K+B) = XR(K+B) + jXI(K+B), X(K) = XR(K) + jXI(K), then: XR(K)+jXI(K)= XR'(K)+jXI'(K)+[ XR'(K+B) + jXI'(K+B)]*[ cos(2πP/N)-jsin(2πP/N)]; further decomposition gives the following two equations: XR(K)= XR'(K)+ XR'(K+B) cos(2πP/N)+ XI'(K+B) sin (2πP/N) (1) XI(K)= XI'(K)-XR'(K+B) sin(2πP/N)+XI'(K+B)cos (2πP/N) (2) It should be noted that: XR(K) and XR'(K) have the same storage location, so after (1) and (2), the value at that location has changed. X'(K) is needed to calculate X(K+B) below, so when programming, be sure to save XR'(K) and XI'(K) into the two temporary variables TR and TI.
Similarly: XR(K+B)+jXI(K+B)= XR'(K)+jXI'(K)- [ XR'(K+B)+jXI'(K+B)] *[ cos(2πP/N)-jsin(2πP/N)]Continue to decompose and get the following two formulas:
② After formula (3), the value of XR(K+B) has changed, and the previous value at this position is used in formula (4), so the previous value XR'(K+B) must be saved before executing formula (3).
③ When programming, XR(K) and XR'(K), XI(K) and XI'(K) use the same variable.
/* Butterfly operation program segment, dataR[] stores the real part, dataI[] stores the imaginary part*/
3 Analysis of the basic idea of DIT FFT algorithm We know that the N-point FFT operation can be divided into LOGN2 levels, each level has N/2 discs. The basic idea of DIT FFT is to use 3 layers of loops to complete the entire operation (N-point FFT). First-level loop: Since N=2m requires m levels of calculation, the first-level loop controls the number of operations. Second-level loop: Since there are 2L-1 butterfly factors (multipliers) at the Lth level, the second-level loop is controlled according to the multipliers to ensure that the third-level loop is executed once for each butterfly factor. In this way, the third-level loop is controlled by the second-level loop, and each level performs 2L-1 loop calculations. The third loop: Since there are N/2L groups in the Lth level, and the multipliers of different groups in the same level have the same distribution, after the second loop determines a multiplier, the third loop will calculate the butterfly with this multiplier once for each group in this level, that is, N/2L butterfly calculations will be performed each time the third loop is executed. We can conclude that in each level, the third loop completes N/2L disk calculations; the second loop makes the third loop perform 2L-1 times, so when the second loop is completed, a total of 2L-1 *N/2L=N/2 disk calculations are performed. In essence, the second and third loops complete the calculation of level L. A few data to note: ① In the Lth level, the two input ends of each disc are b=2L-1 points apart. ② The same multiplier corresponds to N/2L disks with adjacent points spaced 2L apart. ③ The P in the 2L-1 dishing factors WPN of the Lth level can be expressed as p = j*2m-L, where j = 0, 1, 2, ..., (2L-1-1). The above is an analysis and study of the FFT algorithm in embedded systems. Readers can directly apply the algorithm to their own systems. Welcome to write to discuss. (Email: xiaowanang@163.net) Attached is the 128-point DIT FFT function: |
void FFT(float dataR[],float dataI[])
{int x0,x1,x2,x3,x4,x5,x6;
int L,j,k,b,p;
float TR,TI,temp;
/********** following code invert sequence ************/
for(i=0;i<128;i++)
{ x0=x1=x2=x3=x4=x5=x6=0;
x0=i&0x01; x1=(i/2)&0x01; x2=(i/4)&0x01; x3=(i/8)&0x01;x4=(i/16)&0x01; x5=(i/32)&0x01; x6=(i/64)&0x01;
xx=x0*64+x1*32+x2*16+x3*8+x4*4+x5*2+x6;
dataI[xx]=dataR[i];
}
for(i=0;i<128;i++)
{ dataR[i]=dataI[i]; dataI[i]=0; }
/************** following code FFT *******************/
for(L=1;L<=7;L++) { /* for( 1) */
b=1; i=L-1;
while(i>0)
{b=b*2; i--;} /* b= 2^(L-1) */
for(j=0;j<=b-1;j++) /* for (2) */
{ p=1; i=7-L;
while(i>0) /* p=pow(2,7-L)*j; */
{p=p*2; i--;}
p=p*j;
for(k=j;k<128;k=k+2*b) /* for (3) */
{ TR=dataR[k]; TI=dataI[k]; temp=dataR[k+b];
dataR[k]=dataR[k]+dataR[k+b]*cos_tab[p]+dataI[k+b]*sin_tab[p];
dataI[k]=dataI[k]-dataR [k+b]*sin_tab[p]+dataI[k+b]*cos_tab[p];
dataR[k+b]=TR-dataR[k+b]*cos_tab[p]-dataI[k+b]*sin_tab[p];
dataI[k+b]=TI+temp*sin_tab[p]-dataI[k+b]*cos_tab[p];
} /* END for (3) */
} /* END for (2) */
} /* END for (1) */
for(i=0;i<32;i++){ /* Only harmonics below the 32th order are needed for analysis*/
w[i]=sqrt(dataR[i]*dataR[i]+dataI[i]*dataI[i]);
w[i]=w[i]/64;}
w[0]=w[0]/2;
} /* END FFT */
Previous article:Research on Anti-interference Design in Digital Image Processing System Based on DSP
Next article:Design and implementation of a video processing system
Recommended ReadingLatest update time:2024-11-16 17:58



- Popular Resources
- Popular amplifiers
- Huawei's Strategic Department Director Gai Gang: The cumulative installed base of open source Euler operating system exceeds 10 million sets
- Analysis of the application of several common contact parts in high-voltage connectors of new energy vehicles
- Wiring harness durability test and contact voltage drop test method
- Sn-doped CuO nanostructure-based ethanol gas sensor for real-time drunk driving detection in vehicles
- Design considerations for automotive battery wiring harness
- Do you know all the various motors commonly used in automotive electronics?
- What are the functions of the Internet of Vehicles? What are the uses and benefits of the Internet of Vehicles?
- Power Inverter - A critical safety system for electric vehicles
- Analysis of the information security mechanism of AUTOSAR, the automotive embedded software framework
 Professor at Beihang University, dedicated to promoting microcontrollers and embedded systems for over 20 years.
Professor at Beihang University, dedicated to promoting microcontrollers and embedded systems for over 20 years.
- Innolux's intelligent steer-by-wire solution makes cars smarter and safer
- 8051 MCU - Parity Check
- How to efficiently balance the sensitivity of tactile sensing interfaces
- What should I do if the servo motor shakes? What causes the servo motor to shake quickly?
- 【Brushless Motor】Analysis of three-phase BLDC motor and sharing of two popular development boards
- Midea Industrial Technology's subsidiaries Clou Electronics and Hekang New Energy jointly appeared at the Munich Battery Energy Storage Exhibition and Solar Energy Exhibition
- Guoxin Sichen | Application of ferroelectric memory PB85RS2MC in power battery management, with a capacity of 2M
- Analysis of common faults of frequency converter
- In a head-on competition with Qualcomm, what kind of cockpit products has Intel come up with?
- Dalian Rongke's all-vanadium liquid flow battery energy storage equipment industrialization project has entered the sprint stage before production
- Allegro MicroSystems Introduces Advanced Magnetic and Inductive Position Sensing Solutions at Electronica 2024
- Car key in the left hand, liveness detection radar in the right hand, UWB is imperative for cars!
- After a decade of rapid development, domestic CIS has entered the market
- Aegis Dagger Battery + Thor EM-i Super Hybrid, Geely New Energy has thrown out two "king bombs"
- A brief discussion on functional safety - fault, error, and failure
- In the smart car 2.0 cycle, these core industry chains are facing major opportunities!
- The United States and Japan are developing new batteries. CATL faces challenges? How should China's new energy battery industry respond?
- Murata launches high-precision 6-axis inertial sensor for automobiles
- Ford patents pre-charge alarm to help save costs and respond to emergencies
- New real-time microcontroller system from Texas Instruments enables smarter processing in automotive and industrial applications
- Trial record of the super awesome PCB design software kiCad
- EE Hangzhou netizens have a dinner date! Anyone interested on October 22 (Thursday) evening?
- What is the difference between an IoT gateway and an industrial router?
- EMI Issues in Power Converters - Radiated Emissions
- I am working on a paper on an anti-lost device based on 51 and 52 microcontrollers. Can anyone help me?
- [SC8905 EVM Review] + Unboxing test and driver installation
- How to detect inductor saturation | Comment and win a gift!
- Optimizing EMC and Efficiency in High Power DC/DC Converters Part 2
- [McQueen Trial] + Line-following Driving + Ultrasonic Obstacle Avoidance
- Can the freewheeling diode be omitted when the MOS tube controls the solenoid valve?

 MATLAB and FPGA implementation of wireless communication
MATLAB and FPGA implementation of wireless communication













 京公网安备 11010802033920号
京公网安备 11010802033920号