Factors Affecting the Frequency Resolution of Spectrum Analyzers

The spectrum analyzer determines the signal characteristics by measuring the frequency components and amplitude characteristics of the signal. Frequency indicators (frequency range, frequency resolution) and amplitude indicators (dynamic range, distortion, sensitivity) are its important technical indicators. As one of the important measuring instruments for RF and microwave band signals, the spectrum analyzer is widely used to measure the signal level. Harmonic distortion, intermodulation distortion, interference signal elimination, satellite transponder spectrum occupancy, etc., and many users are not very clear about the concept of frequency resolution of spectrum analyzers. This article mainly analyzes the factors affecting the frequency resolution indicators of spectrum analyzers.

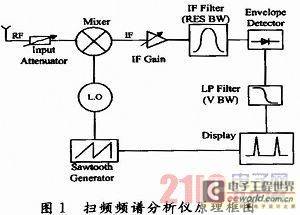
1 Principle of swept spectrum analyzer
Spectrum analyzers can be divided into two categories from the implementation technology of spectrum testing: digital spectrum analyzers using Fourier transform (FFT) technology and analog spectrum analyzers using analog filters (including parallel filter spectrum analyzers and swept spectrum analyzers). Digital spectrum analyzers use numerical calculation methods to process signals of a certain time period, can provide frequency, amplitude and phase information, and can analyze both periodic and non-periodic signals. It is characterized by fast speed and high accuracy, and is suitable for analyzing narrowband signals. The sweeping spectrum analyzer of analog spectrum analyzer is the most common type at present. The superheterodyne method is generally used in the sweeping spectrum analysis. The sweeping spectrum analyzer can analyze stable and periodic signals, provide signal amplitude and frequency information, and is suitable for fast scanning tests with wide bandwidth. Agilent's ESA series economical spectrum analyzers and HP8563 are both sweeping spectrum analyzers. The simplified principle block diagram is shown in Figure 1. The sweeping spectrum analyzer is actually a multi-stage mixing structure. The core part of this analysis method is its mixer and intermediate frequency filter. The mixer downconverts the measured signal to the intermediate frequency, and then processes it at the intermediate frequency to obtain the amplitude. The local oscillator uses a swept oscillator. Its output signal and each frequency component in the measured signal are sequentially difference-converted in the mixer. The generated intermediate frequency signal passes through the intermediate frequency narrowband filter, is amplified and detected, and is added to the video amplifier as the vertical deflection signal of the oscilloscope, so that the vertical display on the screen is proportional to the amplitude of each frequency component. The frequency sweep of the local oscillator is controlled by the sawtooth voltage generated by the sawtooth wave sweep generator. The sawtooth wave voltage is also used as the horizontal scan of the oscilloscope, so that the horizontal display on the screen is proportional to the frequency.

2 Factors affecting the frequency resolution of spectrum analyzers
The frequency resolution of a spectrum analyzer is its ability to distinguish adjacent frequency components. Many signal tests require the spectrum analyzer to have a high frequency resolution. Only when the resolution of the spectrum analyzer is high enough can the characteristics of the signal be correctly reflected on the screen. The frequency resolution of a spectrum analyzer is related to the performance of its internal intermediate frequency filter and local oscillator. The type of intermediate frequency filter, 3 dB bandwidth, frequency selectivity, and the residual frequency modulation and local oscillator phase noise of the local oscillator will affect the frequency resolution of the spectrum analyzer.
2.1 The impact of intermediate frequency filter on frequency resolution
The function of the intermediate frequency filter is to distinguish signals of different frequencies. It is a key part of the spectrum analyzer. It is a narrowband filter with a fixed center frequency. Only by changing the frequency of the swept signal of the local oscillator can the frequency selection be achieved. If the frequency after mixing of the spectrum analyzer falls within the passband of the intermediate frequency filter, the frequency will be displayed on the display. If the frequency after mixing is not equal to the intermediate frequency, it will be blocked by the intermediate frequency filter. The shape of the ideal single-carrier signal displayed in the swept spectrum analyzer test is the frequency response shape of the filter. The shape of the intermediate frequency filter is defined by its bandwidth (3 dB or 6 dB) and frequency selectivity. Its 3 dB bandwidth and rectangular coefficient affect many key indicators of the spectrum analyzer, such as measurement resolution, measurement sensitivity, measurement speed and measurement accuracy.
2.1.1 Impact of resolution bandwidth on frequency resolution
Resolution bandwidth (RES BW) is the 3 dB bandwidth of the intermediate frequency filter, which reflects the ability of the spectrum analyzer to distinguish equal-amplitude signals. When the frequency difference between two equal-amplitude signals is the 3 dB bandwidth of the intermediate frequency filter, the synthetic response curve still has two peaks, and the middle sinks by about 3 dB. They are considered to be distinguishable, so the 3 dB bandwidth of the intermediate frequency filter is called the resolution bandwidth (RES BW) of the spectrum analyzer. HP/AGILENT spectrum analyzers define the 3 dB bandwidth of the intermediate frequency filter as RESBW, and some companies define the 6 dB bandwidth as RES BW. The minimum resolution bandwidth of a spectrum analyzer reflects the grade of the spectrum analyzer. The economical type is 1 kHz to 5 MHz, the multi-functional mid-range type is 30 Hz to 5 MHz, and the high-end type is 1 Hz to 5 MHz. [page]

Figure 2 shows the spectrum of different resolution bandwidths. It can be seen that the carrier shape cannot be distinguished when the resolution bandwidth RBW = 10 kHz, but the carrier shape can be clearly distinguished when the resolution bandwidth RBW = 1 kHz.

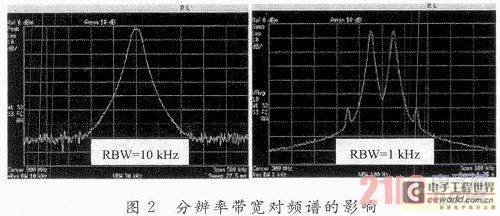
Conclusion: If the interval between the two signals is greater than or equal to the set resolution bandwidth RES BW, the two equal-amplitude signals can be distinguished. If it is less than the selected RES BW, the two signals cannot be distinguished. The smaller the RES BW of the spectrum analyzer, the higher its frequency resolution.
2.1.2 Effect of frequency selectivity on frequency resolution
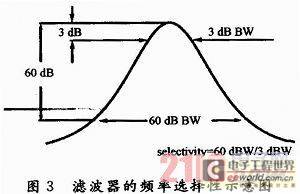
The frequency selectivity of the intermediate frequency filter is the ratio of the 60 dB bandwidth to the 3 dB bandwidth of the intermediate frequency filter, as shown in Figure 3. It reflects the ability of the spectrum analyzer to distinguish signals of unequal amplitude. For two signals with an amplitude difference of 60 dB, the interval must be at least half of the 60 dB bandwidth to distinguish the two signals, otherwise the small signal may be submerged in the skirt of the large signal. The frequency selectivity of the narrowband bandpass filter implemented by digital technology can reach 5:1, and the frequency selectivity of the analog filter can reach 15:1 or 11:1. Figure 3 is a schematic diagram of the frequency selectivity of the filter.

The following example illustrates the effect of different frequency resolution and frequency selectivity on the resolution of unequal amplitude signals. If the RES BW is 3 kHz and the filter frequency selectivity is 15:1, then the bandwidth of the filter down 60 dB is 45 kHz, and half of the 60 dB bandwidth is 22.5 kHz, so the -60 dBc signal 22.5 kHz away from the large signal can be detected. If it is switched to another narrowband filter with a RES BW of 1 kHz and a frequency selectivity of 15:1, then the bandwidth of the filter down 60 dB is 15 kHz, and half of the 60 dB bandwidth is 7.5 kHz, then the ~60 dBc signal 7.5 kHz away from the large signal can be detected. Or switch to another filter with a RES BW of 3 kHz and a frequency selectivity of 5:1, then the bandwidth of the filter down 60 dB is 45 kHz, and half of the 60 dB bandwidth is 7.5 kHz, then the -60 dBc signal 7.5 kHz away from the large signal can be detected. Figure 4 shows the spectrum analyzer measurement results when the frequency filter RES BW = 1 kHz and RES BW = 10 kHz with a frequency selectivity of 15:1. It can be seen that when RES BW = 1 kHz, a -60 dBc signal 7.5 kHz away from the large signal can be detected.

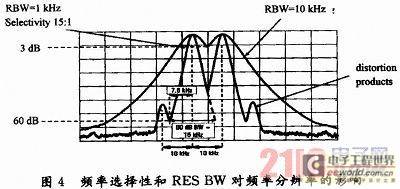
Conclusion: The smaller the frequency selectivity of a spectrum analyzer, the stronger its ability to resolve signals of unequal amplitude. However, the frequency selectivity of a spectrum analyzer is fixed, while the resolution bandwidth is variable. Therefore, when measuring tiny signals, the measurement effect can be achieved by narrowing the resolution bandwidth as much as possible and reducing the average display noise level.