Application of GPS relative positioning in gravity satellite KBR ranging

The Earth's gravity field is a basic physical field of the Earth. The gravity field and its changes reflect the distribution and movement of materials on the Earth's surface and inside, and determine the ups and downs and changes of the geoid. The accurate measurement of the Earth's gravity field is of great significance to the development of disciplines such as geodesy, geophysics, geodynamics and oceanography. The application of satellite gravity measurement technology is of epoch-making significance for the measurement of the Earth's gravity field, and is one of the research frontiers and hot topics in the field of geodesy today. Conventional gravity field determination methods mainly rely on ground gravity observations. The ground
observation period is long, and there is a lack of ocean gravity data, which accounts for three-quarters of the Earth. The accuracy of determining the gravity field is limited. With the development of space positioning technology, the achievements made in the study of the Earth's gravity field in recent years have far exceeded the sum of the past 30 years. The satellite altimetry technology that appeared in the 1980s greatly improved the accuracy of gravity field determination, such as the famous EGM96 model. The gravity satellite GHAMP launched by the German GFZ in July 2000 took an important step in satellite gravity measurement. The low-tracking satellite GRACE, launched jointly by NASA and Europe in March 2002, uses KBR two-way ranging, and uses dual-frequency GPS positioning and timing results to correct KBR ranging, making the ranging accuracy reach tens of microns and the range rate determination accuracy reach 0.1 μm/s. In addition, the European Space Agency also successfully launched the GOCE gravity gradient satellite in March 2009, and satellite gravity measurement has made unprecedented progress. However, my country's research on gravity satellites is currently in its infancy, and the high-precision inter-satellite ranging technology of gravity satellites is also being focused on. To this end, this article mainly introduces the indispensable role of dual-frequency GPS receivers in high-precision inter-satellite ranging of gravity satellites, and proposes an engineering solution for correcting KBR ranging using dual-frequency GPS observations, providing an engineering reference for my country's later satellite gravity detection plans.

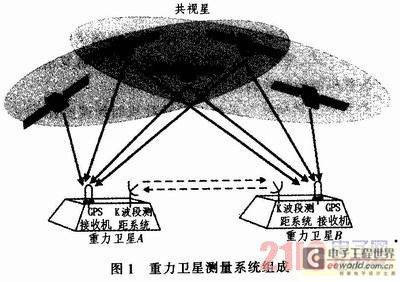
1 Composition of the measurement system
The entire gravity satellite constellation consists of two satellites 200 km apart and at an orbital altitude of 500 km. Each satellite is equipped with a high-precision dual-frequency GPS receiver, a K/Ka dual-band (24/32 GHz) ranging system, and a high-precision clock (the GPS receiver and KBR time standard on each satellite use the same oscillator) as shown in Figure 1. The basic idea of ​​precise ranging between two satellites is: first, use the K-band ranging system (KBR) to measure the distance between the two satellites. At the same time, satellites A and B use their own visible GPS navigation stars for absolute positioning and timing, and then use the common-view GPS navigation stars for relative positioning and timing, and use the GPS relative positioning and timing results to correct the KBR ranging, so that its ranging accuracy reaches the micron level.



2 Correction of KBR ranging with GPS positioning results
2.1 KBR two-way ranging and time synchronization error
The gravity satellites A and B perform precise two-way ranging through the KBR system, and the ranging principle is as follows.
The observation of gravity satellite A on the carrier signal of gravity satellite B at the ideal real time t can be expressed as:

where trA and trB are the KBR time scales of gravity satellites A and B respectively; CA(tr) and CB(tt) are the clock differences of gravity satellites A and B at the signal receiving time and transmitting time respectively; dCA(tr) and dCB(tr) are the clock drifts of gravity satellites A and B at the receiving time respectively. The influence of clock drift on KBR phase only occurs in the period from signal transmission to reception (r≈0.7 ms). As long as the clock drift reaches 10-10, the phase measurement accuracy of 1/1000 cycle can be achieved. Therefore, the main error affecting the phase measurement accuracy is the synchronization error of the time scales ttA and trB. [page]

2.2 Dual-frequency GPS observations correct KBR ranging errors
For gravity satellite constellations, in order to meet the accuracy of gravity field measurement with a spatial resolution of several hundred kilometers, the ranging accuracy between two satellites must reach several microns. The satellite's KBR uses a 32.7/24.5 GHz frequency signal (wavelength of about 1 cm), so the phase measurement accuracy must reach one thousandth of a cycle (1/1 024). The difference frequency signals after modulation are 502 and 670 kHz respectively. In order to ensure the phase measurement accuracy of 1O-4 cycles, the timing accuracy should reach 10-4/670 kHz=150 ps (0.15 ns), which is almost impossible for an on-orbit oscillator. Using IGS products and the precise orbit determination (POD) technology, the absolute time scale of KBR measurements and the position of the satellite can be determined. The position accuracy can reach 2 to 3 cm, and the timing accuracy can reach 0.1 ns, which can meet the requirements of the KBR time scale. Therefore, the GPS ground data processing system is one of the key technologies for KBR to achieve micron-level accuracy. The main tasks of the GPS receiver on the gravity satellite are:
1) to restore the gravity field of the long-wavelength term using the centimeter-level precision perturbation orbit of the carrier satellite determined by GPS;
2) to eliminate the long-term clock drift of the onboard oscillator
using the absolute timing results of GPS; 3) to calibrate the synchronization error of the K-band ranging using the relative timing results of GPS, with an accuracy of 0.1 ns (3 cm).
In general, the relative positioning and relative timing adopt a post-processing scheme, using the GPS dual-frequency carrier phase observation value as the basic observation value, supplemented by carrier phase smoothing pseudorange, dynamic smoothing and other processing methods to obtain the ambiguity fixed coordinate solution. First, the observation data is quality checked, the possible cycle slip of the carrier phase is corrected, and the observations with gross errors are eliminated. The one-day observation arc is used as the processing unit, extending 3 hours forward and backward, that is, from 21:00 of the previous day to 3:00 of the next day, a total of 30 hours, in order to interpolate the GPS satellite IGS precise ephemeris.
The key to relative positioning using carrier phase is to correctly determine the integer ambiguity. The use of integer solutions can improve the stability and accuracy of the coordinate solution. However, in order to eliminate the ionospheric error, the L3 combination must be used, and L3 does not have an integer solution. The phase measurement pseudorange double difference observation equation (expressed in distance) can be transformed into:

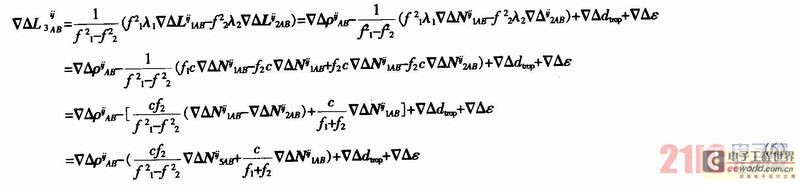
In the formula, it is essentially a double difference wideband ambiguity with integer characteristics. If it can be fixed by other means, then the ambiguity unknowns in L3 only exist in the double difference ambiguity of L1, and it should be an integer, and its coefficient is exactly equal to the wavelength of the narrow wave (11 cm), so L3 is converted into an observation model with integer ambiguity estimation. The wideband double difference ambiguity can be solved jointly by the wideband double difference and Melbourne-Wubbena combination.
Since the accuracy of carrier phase measurement is much higher than the accuracy of pseudorange measurement, high-precision time synchronization can be achieved through carrier phase measurement. Relative timing uses a single difference mode. Due to the existence of receiver clock error, it is difficult to obtain an integer solution for the single difference ambiguity. To this end, precise relative positioning is first performed to obtain differential positioning results and baseline variances with an accuracy of 1 to 2 cm. Secondly, the baseline result is substituted into the single difference observation equation as a coordinate parameter with a priori precision information, so as to solve the high-precision relative clock error.
The single difference observation equation of the carrier phase between the two satellite-borne GPS receivers can be expressed as:

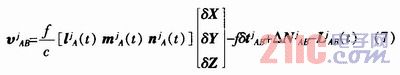
where is the measurement residual, is the position coordinate correction vector of the satellite-borne GPS receiver A, is the clock deviation between the satellite-borne GPS receiver A and the satellite-borne GPS receiver B, and is the single difference ambiguity.
The clock deviation between the two satellite-borne GPS receivers can be obtained by equation (7):

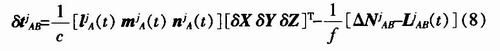
The position coordinate correction vector of GPS receiver A is obtained by precise relative positioning using the double-difference carrier phase, which is substituted into the above equation as a coordinate parameter with a priori precision information, and the single difference ambiguity is searched out, and the clock deviation between the two satellite-borne GPS receivers can be solved.
However, since the ambiguity is coupled with the satellite-borne GPS receiver clock error and the GPS satellite clock error, the single difference equation only eliminates the influence of the GPS satellite clock error, and the problem of the unknown initial phase of the satellite-borne GPS receiver still exists, so the single difference ambiguity cannot be solved in the form of an integer cycle. To this end, the single-difference equation needs to be reintegrated. Assuming that the rth GPS satellite is selected as the reference satellite, represented by the superscript ref, equation (8) can be written as:

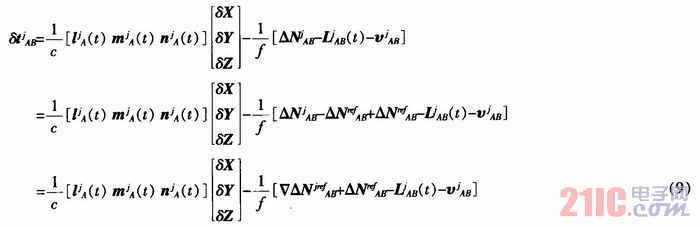
After the above reintegration, the in the equation becomes a double-difference ambiguity, which satisfies the integer characteristics of the ambiguity. The integer ambiguity search method can be used for search, where the double-difference ambiguity of the reference satellite becomes zero, and its single-difference ambiguity is a constant quantity that can be estimated by least squares.
When studying precise relative timing, it is also necessary to consider the influence of the absolute clock error of the reference station on the relative timing. Therefore, the absolute clock error of the reference station can also be considered first. At present, the absolute clock error accuracy of the GRACE satellite determined by JPL using the ground high-precision time reference benchmark reaches 0.1 ns. In the absolute timing process, the influence of relativity must also be considered.
Through the above process, the GPS relative positioning and timing results can be used to eliminate the long-term clock drift of the satellite-borne oscillator and calibrate the synchronization error of the K-band ranging, so that the KBR ranging reaches the micron level. [page]
3 Simulator test verification
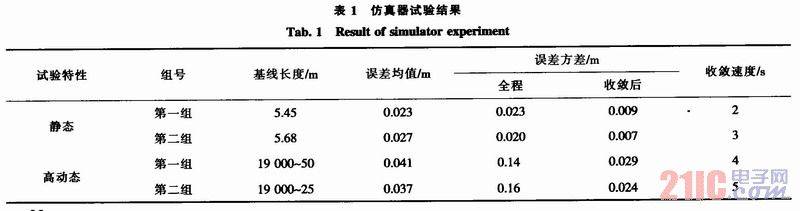
In order to verify the feasibility and positioning accuracy of the above method, simulator static and high dynamic tests were designed. The dual-frequency data of the simulator is received by a dual-frequency receiver, and the original observation data is processed by the dual-frequency relative positioning software and compared with the theoretical value to verify the accuracy. The test method is shown in Figure 2. The relative measurement results of each test are shown in Table 1.

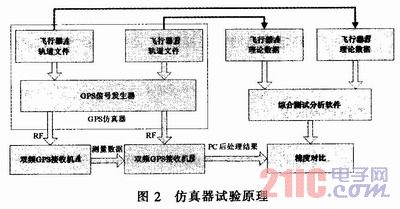
3.1 Static test
In order to verify the performance of the dual-frequency relative measurement algorithm, the static baseline test is first used to verify it. There are two groups of tests. The simulator outputs the static baseline dual-frequency signal, and the dual-frequency relative positioning software is used to post-process the original observations. The processing results are compared with the theoretical data, and the results are shown in Figures 3 and 4.


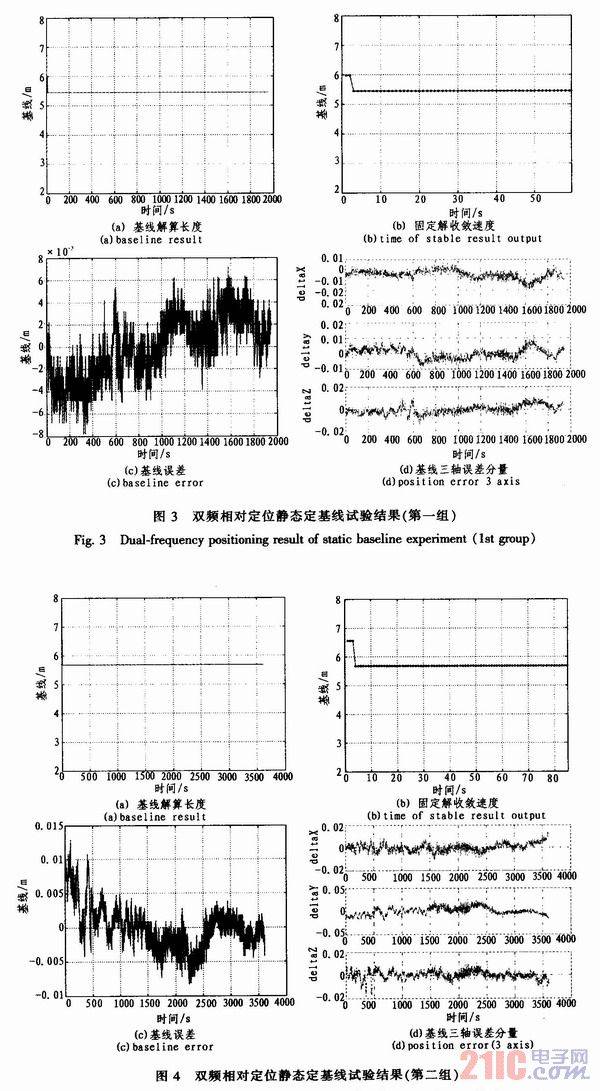
From the analysis results of the above two groups of tests, it can be seen that the dual-frequency relative positioning software can be used to stably solve the baseline. The baseline solution results are consistent with the theoretical values. After the fixed solution converges, the error can be controlled within 2 cm. As can be seen from Figures 3(a) and 4(a), the baseline solution errors of the initial few epochs are large. This is because the floating-point solution has not converged yet, and due to the ill-conditioned nature of the carrier phase double-difference observation equation under static conditions, a small measurement error will lead to a large positioning error. With the increase of observation epochs, the ill-conditioned nature of the equation is improved, and the floating-point solution gradually converges to a stable real number solution. After the floating-point solution converges and the ambiguity integer solution is fixed, a stable and high-precision solution can be obtained, and the accuracy is less than 1 cm. [page]

3.2 High dynamic test
In order to verify the performance of the dual-frequency relative measurement algorithm under high dynamic conditions, a high dynamic test was designed. The performance of the algorithm under high dynamic conditions was verified by using the simulator high dynamic orbit, and the original observations were processed with the dual-frequency relative positioning software. The processing results were compared with the theoretical data, and the results are shown in Figures 5 and 6.


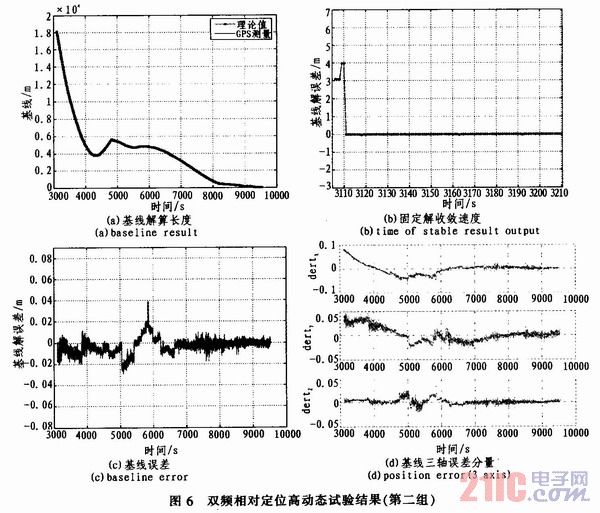
Through the high dynamic test, it can be found that the dual-frequency GPS precision relative measurement algorithm can stably perform baseline solution, and the solution results are consistent with the theoretical values. After the positioning converges, the algorithm can stably output high-precision relative positioning results, and the error variance is less than 3 cm.

4 Conclusion
The precise measurement of the Earth's gravity field is of great significance to the development of disciplines such as geodesy, geophysics, geodynamics and oceanography. High-precision GPS relative positioning and timing are the basic prerequisites for ensuring the KBR ranging accuracy and thus ensuring the spatial resolution of the Earth's gravity field measurement. By analyzing the role of onboard GPS in the gravity satellite KBR ranging mission, this paper designs a dual-frequency combination method for engineering application, and gives an ambiguity resolution method suitable for actual engineering. The simulator test verifies that the solution convergence time of this method is less than 5 s under both static and high dynamic conditions, and the positioning accuracy is less than 3 cm after the solution is stable, which can meet the requirements of using GPS results to correct KBR ranging.